Сумма двух длин сторон - 96/2=46;
46-4=42 - сумма сторон при условии что они равны между собой;
42/2=21 ед. - одна сторона;
21+4=25 ед. - другая сторона (большая).
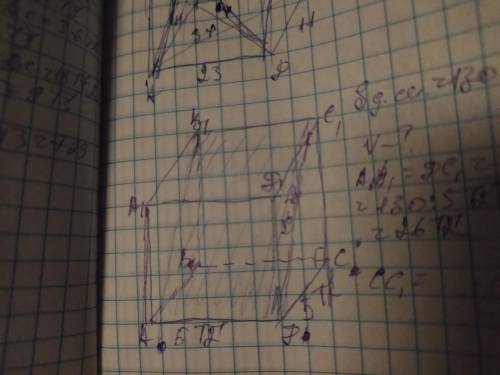
В основе правильной четырёхугольной призме лежит квадрат. Диагональным сечением призмы является прямоугольник, и так как известна его площадь, найдём его вторую сторону по формуле обратной формуле площади:
АВ1=ДС1=130÷5√2=26√2см
Вторая сторона диагонального сечения также является диагональю в гранях АА1В1В и ДД1С1С. Диагональ делит эти грани на 2 равных прямоугольных треугольника, в которых сторона основания и высота призмы являются катетами а диагональ гипотенузой. Зная сторону и диагональ найдём высоту призмы по теореме Пифагора:
ДД1²=С1Д²-СД2=(26√2)²-(5√2)²=
=676×2-25×2=1352-50=1302; ДД1=√1302см
Теперь найдём объем призмы, зная стороны и высоту по формуле:
V=а²×h, где а- стороны основания, а h-высота призмы:
V=(5√2)²×√1302=25×2×√1302=
=50√1302см³
ОТВЕТ: V=50√1302см³
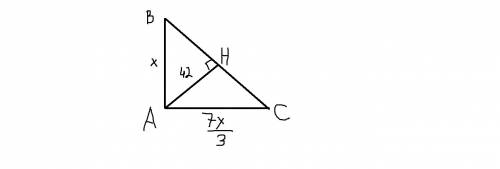
Пусть меньшая сторона - х, тогда большая - х+4, P=(a+b)*2, составим уравнение
(х+х+4)*2=92
2х+4=92:2
2х+4=46
2х=46-4
2х=42
х=42:2
х=21 - меньшая сторона
21+4=25 - большая сторона
проверка (21+25)*2=92