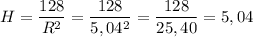Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

R≅5,04
H≅5,04
Объяснение:
Объём цилиндра :
(1) V = πR²H,
где R - радиус цилиндра, H - высота цилиндра.
Площадь полной поверхности цилиндра:
(2) S = πR² + 2πRH
Выразим из формулы (1) высоту цилиндра и подставим значение в формулу (2):
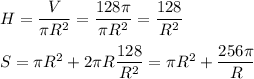
Найдём минимум этой функции по переменной R. Для этого вычислим производную и определим критические точки.
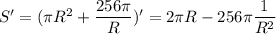 .
.
S' = 0,
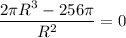
Если R = 0, то производная не существует.
![2\pi (R^3-128)=0\\\\R^3 = 128\\\\R=\sqrt[3]{128}](/tpl/images/2088/5757/d960d.png)
R≅ 5.04
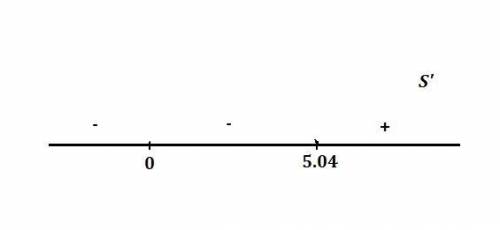
Отметим эти значения на координатной прямой и oпределим знак производной на трёх полученных числовых интервалах. (Cм.рис)
Известно, что в точке минимумa производная меняет знак с минусa на плюс. Соответственно, наименьшее количество материала можно получить, если радиус основания цилиндра R=5,04
Вычислим соответствующую высоту цилиндра: