Я очень люблю мир Геометрии, ведь здесь мы узнаём много нового и интересного! Надеюсь я вам! Знаю что одно предложение, но больше я не придумал.
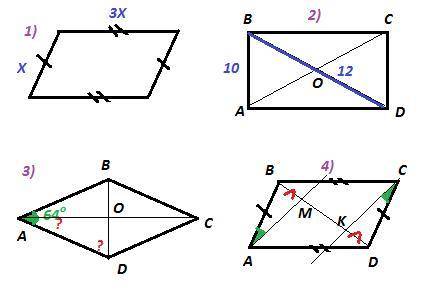
1) Противоположные стороны параллелограмма равны. Пусть две меньшие стороны параллелограмма по Х см, тогда две другие по 3Х см.
2 (X + 3X) = 72; 8X = 72
X = 9 см ; 3X = 27 см
ответ: 9 см, 9 см, 27 см, 27 см
2) Диагонали прямоугольника равны и точкой пересечения делятся пополам
AO = BO = CO = DO = BD : 2 = 12 : 2 = 6 см
Противоположные стороны прямоугольника равны
CD = AB = 10 см
 = CD + CO + DO = 10 + 6 + 6 = 22 см
= CD + CO + DO = 10 + 6 + 6 = 22 см
3) Диагонали ромба делят углы ромба пополам.
Пусть ∠BAD = 64° ⇒ ∠DAC = ∠BAC = 64° : 2 = 32°
Диагонали ромба пересекаются под прямым углом ⇒
ΔAOD - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90° ⇒
∠ADO = 90° - ∠DAO = 90° - 32° = 58°
ответ : 32° и 58°
4) Противоположные стороны параллелограмма параллельны и равны. Рассмотрим ΔABM и ΔCDK.
AB = CD - противоположные стороны параллелограмма;
∠BAM = ∠DCK - по условию;
∠ABM = ∠CDK - накрест лежащие углы при AB║CD и секущей BD
⇒ ΔABM = ΔCDK по стороне и двум прилежащим к ней углам.
⇒ BM = DK как стороны в равных треугольниках, лежащие против равных углов.

Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик) , от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус» , а термин «линия» возник от латинского «линум» (льняная нить) .
Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами; при изготовлении технических чертежей — выполнять геометрические построения. И если ты, юный читатель, хорошо изучил курс геометрии, то не останешься безоружным, когда при решении практических задач потребуется применить геометрические теоремы или формулы.