15
Объяснение:
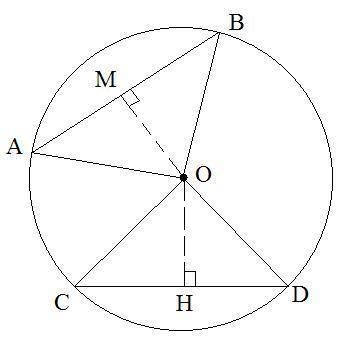
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15
15
Объяснение:
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15

1. В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона.
Дано: ΔАВС, АВ > ВС.
Доказать: ∠С > ∠А.
Доказательство: На стороне АВ отложим отрезок ВК = ВС.
ΔВКС равнобедренный, значит ∠ВКС = ∠ВСК.
∠ВКС - внешний для треугольника АКС, а значит больше каждого внутреннего угла, не смежного с ним, т.е. ∠ВКС > ∠А, тогда и ∠ВСК > ∠А.
∠ВСК < ∠С, ⇒ ∠С > ∠А.
Второе утверждение:
Дано: ∠С > ∠А.
Доказать: АВ > ВС.
Доказательство: (от противного).
Предположим, что АВ < ВС, но тогда по тервой части теоремы ∠С < ∠А. Противоречие.
Предположим, что АВ = ВС. Но тогда ∠С = ∠А как углы при основании равнобедренного треугольника. Противоречие.
Значит АВ > ВС.
2.
1) Все равнобедренные треугольники равны.
Неверно.
2) В прямоугольном треугольнике сумма углов, прилежащих к гипотенузе, всегда равна 90 градусов.
Верно.
Теорема: Сумма острых углов прямоугольного треугольника равна 90°.
Дано: ΔАВС, ∠С = 90°.
Доказать: ∠А + ∠В = 90°.
Доказательство:
Сумма углов треугольника равна 180°:
∠А + ∠В + ∠С = 180°
∠А + ∠В = 180° - ∠С
∠А + ∠В = 180° - 90° = 90°
3) Все точки каждой из двух параллельных прямых по разному удалены от другой прямой.
Неверно. Одинаково удалены.