И.к противоположные углы параллелограмма равны,а угол b=2a, то составим уравнение. B=x,тогда а=2х.
x+2x+x+2x=360
6x=360
x=60
A и С= 60, а В и D= 120
1) 1. рассмотрим АДС-прямоугольный (АД-высота) АД=24см ДС=18см . по тПифагора СА=sqrt24^2+18^2=30cm
2. из соотношения сторон и высоты к гипотенузе прямоугольного треугольника имеем
АС^2=CD*CB CB=AC^2 / CD CB=30^2 / 18= 50cm ДВ=50-18=32см
АВ^2 =DB*CB AB^2=50*32=1600cm^2 AB=40cm
можно было проще : египетский треугольник , соотношение сторон 3:4:5
у АВС АС=30см СВ=50см АС:АВ:СВ =3:4:5=30 :40:50 АВ= 40см
3. сos A -?????? cos90* =0
cosCBA= BA /BC cosBCA=CA/BC cosBAD=BD / BA cosDAC=DA/CA =24 /30=4/5
подставь длинну катета и гипотенузы и вычисли
2) АВСД- трапеция угА=угВ=90*, ВС=3см, СД=4см угВСД=150*
1)проведем СН-высота угВСН=СНА=90* угНСД=150*-90*=60* АН=3см
2)рассмотрим треугольник НСД-прямоугольный угСНД=90* угНСД=60* значт угНДС=30*
напротив угла 30* лежит сторона = 1/2 гипотенузы , отсюда СН=1/2СД =2см
по т Пифагора НД=sqrt (4^2-2^2)=2sqrt3 (2 корня из3)
3) Sтрап =( (a+b) /2 ) * h
S(ABCD) = (3+3+2sqrt3) / 2) *2 =(6+2sqrt3) cm^2
3) Sпрямоуг= а*в
пусть а=АД в=СД
рассмотримАСД-прямоугольный угД=90* САД=37* cos37*= a /c sin37*=b/c
a=3 cos37* b=3 sin37*
S= 3 cos37* * 3 sin37* = 9 * 1/2 sin(37*2)= 4.5 sin74*
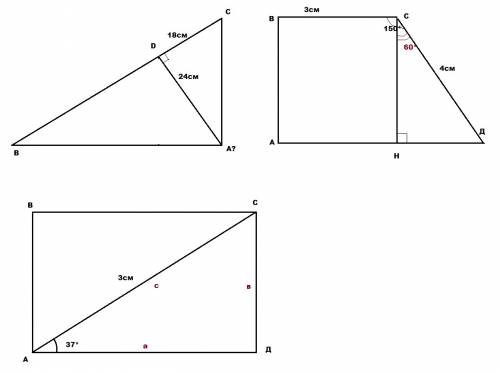
1) Высота прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы
отрезок ДС, равный 18 см.
Найдите АВ и cos А.
Катет прямоугольного треугольника есть среднее пропорциональное между
гипотенузой и проекцией этого катета на гипотенузу.
Проекция АД катета АВ на гипотенузу равна разности между длиной гипотенузы и длиной отрезка ДС
АД= АС-ДС=24-18=6 см
АВ²=6*24=144
АВ=√ 144=12
cos А=АД:АВ=6:12=1/2
2) В прямоугольной трапеции меньшее основание равно 3 см, большая боковая
сторона равна 4 см, а один из углов трапеции 150градусов. Найдите площадь
трапеции.
Угол 150° - угол при большей боковой стороне.
Сумма углов при каждой боковой стороне трапеции равна 180°.
Острый угол, образованный этой стороной и основанием равен
180°-150°=30°.
Опустим высоту из тупого угла на большее основание трапеции.
Так как высота противолежит углу 30°, ее длина равна половине длины боковой стороны и равна 4:2=2 см
Высота равна меньшей боковой стороне, так как трапеция прямоугольная, и она отсекла от трапеции треугольник ( из которого мы находили ее величину) и прямоугольник со сторонами, равными высоте и меньшему основанию.
Большее основание равно меньшему основанию плюс длина катета прямоугольного треугольника, образованного высотой и боковой стороной.
Найдем длину этого катета по теореме Пифагора:
х²=4²-2² =16-4=12
х=2√3
Большее основание равно 3+2√3
Площадь трапеции равна ½ произведения ее высоты на сумму оснований.
S=2·( 3+3+2√3):2= 6+2√3=2(3+√3) cм²
3) Диагональ АС прямоугольника АВСД равна 3 см и составляет стороной АД угол
37°.Найдите площадь прямоугольника АВСД.
Прямоугольник - параллелограмм.
Формула площади параллелограмма через диагонали и угол между ними
S=(D·d·sin α ):2
S=(D·d·sin β ):2 ( синусы углов, дополняющих друг друга до 180°, равны )
D - большая диагональ
d - меньшая диагональ
α, β - углы между диагоналями
Диагонали АС и ВД прямоугольника равны. Точкой пересечения они делятся пополам. Поэтому с каждой из сторон они образуют равнобедренные треугольники АОД и АОВ, в которых боковые стороны - половина диагонали, основание - сторона прямоугольника.
Пусть угол АОД = α
Угол α между диагоналями равен 180°-2*37°=106°.
Sin(106°)= 0.9613
S=(3·3·0.9613):2 ≈ 4,33 см²
2. Сумма углов в четырёхугольнике равна 360 градусов. Тогда 6А=360, А=60 градусов, а В=2×60=120.
ответ: 60,60,120,120