"1. На луче с началом в точке А отмечены точки В и С. Известно, что AC = 7, 8см, ВС = 2,5 см. Какую длину может иметь отрезок АВ?
2. Луч BP проходит между сторонами угла ABC. Найдите угол РВС, Если угол ABC равен 83 , угол АВР равна 48
3. Один из двух углов, образованных при пересечении двух прямых, на 22 меньше второго. Найдите все образовавшиеся углы.
4. Один из смежных углов в 4 раза меньше второго. "
1) АВ=АС-ВС.
АВ=7,8-2,5=5,3 см.
2) ∠РВС=∠АВС-∠АВР=83*-48*=35*.
3) Меньший угол обозначим через х. Тогда больший будет х+22*
Эти углы смежные и их сумма равна 180*.
х+х+22*=180*.
2х=158*.
х=79*. - меньший угол.
79*+22*=101* - больший угол.
ответ: При пересечении двух прямых образовалось четыре угла: два смежных 79* и 100* и два накрест лежащих: 79*=79* и 101*=101*.
4) меньший угол обозначим через х. Тогда больший будет 4х. Сумма смежных углов равна 180*.
х+4х=180*.
5х=180*.
х=36* - меньший угол.
Больший угол равен 36*4=144*
ответ: 36* и 144*( 36*+144*=180*)
Уже решала такую же точно задачу, только сторона в ней равна не 1, а 2.
----------------------------------------------------------------
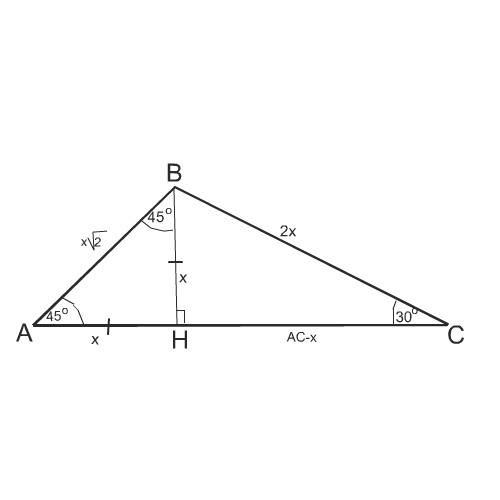
Сделаем рисунок к задаче.
Пусть сторона, к которой прилежат углы, данные в условии, будет основанием АС треугольника АВС.
Из вершины В опустим к АС высоту ВН.
С ее мы отсекаем от треугольника АВС равнобедренный прямоугольный треугольник АВН.
Угол ВАС=45° по условию,
Угол АВН - из прямоугольного треугольника АВН.
Обозначим катеты ВН и АН этого треугольника х ( так как они равны).
Тогда НС=1-х
а сторона ВС, как гипотенуза треугольника ВНС, равна 2х, так как в этом треугольнике катет, противолежащий углу 30°, равен х,
Составим уравнение по теореме Пифагора для стороны ВС треугольника ВНС.
ВС²=НС²+ВН²
4х²=х²+(1-х)²
4х²=х²+1-2х+х ²
2х²+2х-1=0
Решим квадратное уравнение
D=b²-4ac=2²-4·2·(-1)=12
х₁= (-b+√D):2а= (- 2 +√12):4= -2(1- √3):4=( √3-1):2
х₂= -1,366 и не подходит.
АВ=( √3-1):2)√2=( √6- √2):2≈(2,449-1,414):2≈0,52
ВС=2·( √3-1):2 ≈0,732
180-47 градусов и 18 минут=132 градуса 42 минуты