В правильном тетраэдре все грани - равные равносторонние треугольники.
Площадь одной грани:
S₁ = a²√3/4 = 4²√3/4 = 4√3 см²
Так как К - середина DC, то АК = ВК - медианы и высоты равных треугольников DAC и DBC. Тогда
Sakd = Sbkd = 1/2 S₁ = 2√3 см² - это площади двух боковых граней пирамиды KABD.
Пусть Н - середина АВ, так как треугольник АКВ равнобедренный, то КН - его высота.
СН = DH = а√3/2 = 4√3/2 = 2√3 см как медианы и высоты равных равносторонних треугольников.
Тогда ΔDHC равнобедренный, КН - его медиана и высота:
КН⊥CD.
ΔСКН: ∠СКН = 90°, СН = 2√3 см, СК = CD/2 = 2 см, по теореме Пифагора
КН = √(CH² - CK²) = √((2√3)² - 2²) = √(12 - 4) = √8 = 2√2 см
Sabk = 1/2 AB · KH = 1/2 · 4 · 2√2 = 4√2 см²
Площадь боковой поверхности пирамиды KABD:
Sбок = Sakd + Sbkd + Sabk = 2√3 + 2√3 + 4√2 = 4(√3 + √2) см²
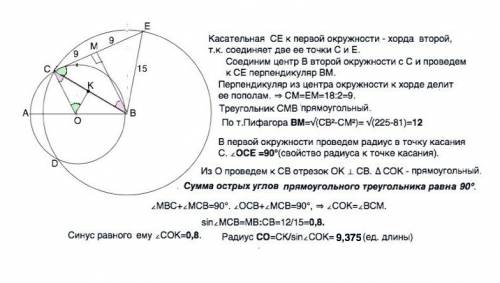
Касательная СЕ к первой окружности - хорда второй, т.к. соединяет две ее точки С и Е.
Соединим центр В второй окружности с С и проведем к СЕ перпендикуляр ВМ.
Перпендикуляр из центра окружности к хорде делит ее пополам. ⇒ СМ=ЕМ=18:2=9. Треугольник СМВ прямоугольный.
По т.Пифагора ВМ=√(СВ²-СМ²)= √(225-81)=12
В первой окружности проведем радиус в точку касания С. ∠ОСЕ =90°(свойство радиуса к точке касания).
Из О проведем к СВ отрезок ОК ⊥ СВ. ∆ СОК - прямоугольный. Сумма острых углов прямоугольного треугольника равны 90°.
∠МВС+∠МСВ=90°. ∠ОСВ+∠МСВ=90°, ⇒ ∠СОК=∠ВСМ. sin∠МСВ=МВ:СВ=12/15=0,8. Синус равного ему ∠СОК=0,8.
Радиус СО=СК/sin∠COK= 9,375 (ед. длины)
Треугольник МNР равнобедренный, так как у ромба стороны равны. значит отрезок NO является и биссектрисой и медианой треугольника. Угол N делит пополам. Так как NO медиана угол NOM равен 90. Угол NMO=(360-200)\4=40градусов. Угол ONM =50