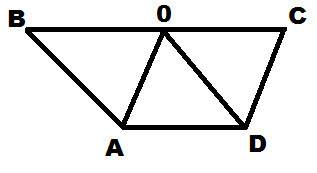
а) ABOD – параллелограмм.
Верно. АВ║OD по условию, AD║ВО, так как лежат на параллельных основаниях трапеции. Если в четырехугольнике противоположные стороны параллельны, то это параллелограмм.
б) ABOD – ромб.
Верно. Так как если в параллелограмме смежные стороны равны, то это ромб.
в) AOCD – ромб.
Неверно. АО║CD по условию, ОС║AD так как лежат на параллельных основаниях трапеции. Значит AOCD - параллелограмм. Но смежные стороны в нем не равны (AD ≠ AO по условию), значит это не ромб.
г) ∠COD=∠AOD
Неверно. Диагональ параллелограмма не является биссектрисой его углов.
д) ∠AOD=∠BOA
Верно, так как диагонали ромба лежат на биссектрисах его углов.
Построим параллелограмм АВСD и проведем биссектрису из угла ВАD к стороне ВС, точку пересечения с прямой обозначим Е.
ВС параллельна AD по свойству параллелограмма, угол EAD равен углу ВЕА, т.к. они являются накрест лежащими. Угол ВАЕ=ЕАD (т.к. АЕ - биссектриса)⇒угол BEA= углу BAE ⇒ треугольник АВЕ - равнобедренный (т.к. его углы равны)⇒ ВЕ=АВ=9 см
Так как АВ=CD по свойству параллелограмма, а ВС равна сумме двух отрезков, на которые её поделила биссектриса (9+14=23 см), находим периметр параллелограмма:
23+23+9+9=64 см
Вроде бы так