
Подробно.
Пусть данный ромб АВСД.
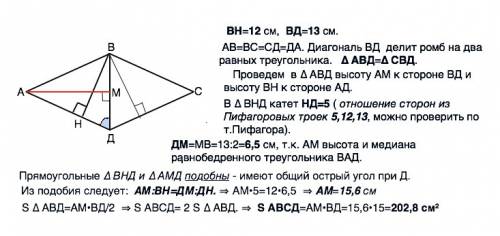
Высота ВН=12 см, диагональ ВД=13 см.
Стороны ромба равны.
Диагональ ромба делит его на два равных треугольника.
∆ АВД=∆ СВД.
Проведем в равнобедренном ∆ АВД высоту АМ к стороне ВД и высоту ВН к стороне АД.
В ∆ ВНД катет НД=5 ( отношение сторон из Пифагоровых троек 5,12,13, можно проверить по т.Пифагора).
ДМ=МВ=13:2=6,5 см, т.к. АМ высота и медиана равнобедренного треугольника ВАД.
Прямоугольные ∆ ВНД и ∆ АМД подобны - имеют общий острый угол при Д.
Из подобия следует:
АМ:ВН=ДM:ДH.
АМ•5=12•6,5
AM=15,6 см
S ∆ АВД=АМ•ВД/2
S АВСД= 2 S ∆ АВД.
S АВСД=АМ•ВД=15,6•15=202,8 см²
Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.