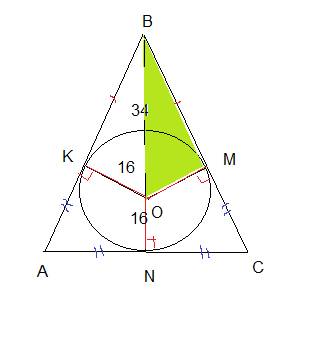
Стороны треугольника являются касательными к окружности.
Касательная перпендикулярна радиусу, проведенному в точку касания.
ОК⊥АВ
OL⊥AC
Высота равнобедренного треугольника, проведённая к основанию, одновременно и медиана и биссектриса.
AL=LC
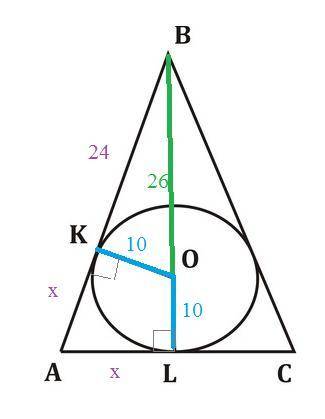
ОК=ОL=10 см
BO=26 см
По теореме Пифагора
BK²=BO²-OK²=26²-10²=676-100=576
BK=24 см
Пусть AK=x
По свойству касательных, проведенных к окружности из одной точки
AK=AL=x
По теореме Пифагора из прямоугольного треугольника АВL:
AB²-AL²=BL²
(24+x)²-x²=(10+26)²
24²+48x+x²-x²=36²
48x=720
x=15
AC=2AL=30 см
S(Δ ABC)=(1/2)AC·BL=(1/2)·30·36=540 кв см.
Проведи биссектрисы. Получим треугольник. В него входят половины углов, значит сумма этих половин будет 45°. Тогда третий угол треугольника равен 180-45=135°. Это и есть угол между биссектрисами. Если нужен второй угол между биссектрисами то он будет смежный с найденным и равен 135°. Выбираем либо В, либо D.
Я предпочту ответ В. Он острый.