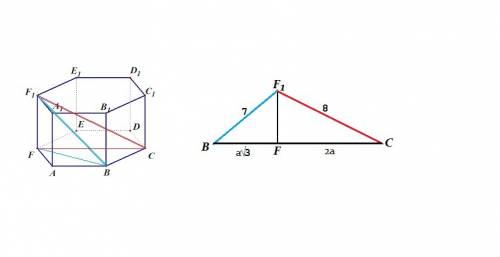
Катет АС противолежит углу 30° и равен половине гипотенузы АВ.
АС=5 см.
Окружность и прямая могут касаться и иметь одну общую точку, не касаться и не иметь общих точек, или пересекаться, при этом они будут иметь две общие точки .
1) радиус, проведенный в точку касания, равен катету r=АС =5 см( т.к. угол ВСА=90°, а радиус перпендикулярен касательной в точке касания)
2) Окружность не будет касаться прямой ВС, если её радиус меньше катета АС. r < AC; r < 5 см
3) Окружность и прямая пересекутся, если радиус больше расстояния от центра окружности до прямой. r > AC' r > 5 см
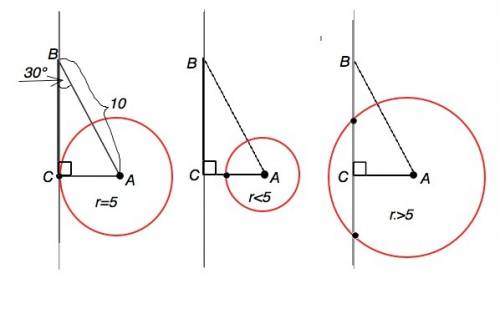
Так как ABCD - параллелограмм, AB параллельна CD, значит угол AKD =CDK , как накрест лежащие углы при параллельных прямых AB и CD, с секущей KD.
угол AKD=ADK, AKD=CDK, следовательно угол ADK = CDK, следовательно DK -биссектриса, чтд.
ABCD - параллелограмм, следовательно AB=BC.
Из доказанного - AD=AK
AD=BC, AD=AK, следовательно AD=AK=BC=4
AB=AK+KB=4+3=7
AB=CD=7, т к ABCD -параллелограмм
P=(4+7)*2=11*2=22