2) Пусть средняя линия MN. N- середина ВС, аналогично пункту 1 находим координаты точки N: ((-1+8)/2;(2-4)/2; (3+9)/2) или (3,5;-1;6). Тогда длина отрезка MN равна корню квадратному из выражения (3,5-3)2+(-1+2)2+(6-5)2 (тут каждая скобка в квадрате!), равно корню квадратному из 2,25 или просто 1,5.
3) Для нахождения координаты вершины D параллелограмма ABCD составьте выражения: длина отрезка АС равна длине отрезка BD, т.е. (8+2)2+(-4-0)2+(9-1)2=(x+1)2+(y-2)2+(z-3)2, где (x;y;z) - координаты точки D. Аналогично выражения: длина отрезка АВ равна длине отрезка CD. А потом, например, длина отрезка AN равна длине отрезка ND. Составьте и решите систему из трех уравнений с тремя неизвестными
Рисунок прикреплён
Средняя линия равна половине суммы оснований..
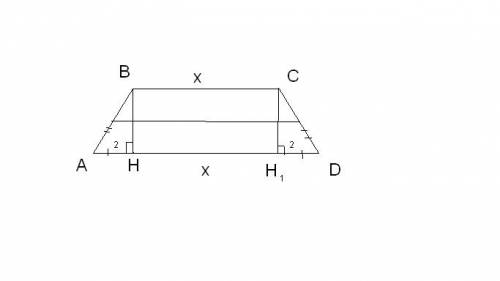
У нас проведена высота. проведём из второго тупого угла ещё одну высоту. в итоге бОльшее основание разделится на три части, две из которых будут равны, т.е. AH=AH₁=2, т.к. трапеция равнобедренная.
Из рисунка видно, что третья часть и меньшее основание равны. BC=HH₁
Пусть меньшее основание будет равно x (BC=x) , тогда средняя линия будет равна:
(x+2+2+x)/2=(2x+4)/2
где 2x - сумма меньшего основания и третьего отрезка бОльшего основания.
Средняя линия равна 8, тогда приравниваем
(2x+4)/2=8
2x+4=8×2
2x+4=16
2x=16-4
2x=12
x=12/2
x=6
Большее основание будет равно AD=6+2+2=10
ответ, большее основание равно 10 см.
Теперь всё по порядку:
AH=AH₁=2
BC=HH₁=x
(x+2+2+x)/2=(2x+4)/2
(2x+4)/2=8
2x+4=8×2
2x+4=16
2x=16-4
2x=12
x=12/2
x=6
AD= 6+2+2=10
Рисунок прикреплён
Прямоуг-АВСD
АВ n CD= О
AB перпендикулярно СД,
СД перпенд АВ =>
АО=ОС=ВО=ОД
ТК диаг равны и пересёк под углом 90 то АВСD крэвадрат
ответ: АВСД-квадрат