3.1) Так как медиана прямоугольного треугольника, проведенная к гипотенузе равна ее половине, AB = 2 * CM = 2 * 6 = 12 см
2) Так как CM = AM, треугольник АСМ - р/б ⇒ ∠MAC = ∠ACM = 50°
∠ACB = 90° ⇒ ∠BCM = 90 - 50 = 40°
3) Так как сумма углов треугольника равна 180°, ∠AMC = 180 - 50 - 50 = 80°
4.1) Так как CP - биссектриса (т.е. делит угол пополам), ∠ACP = 90 ÷ 2 = 45°, и тогда ∠A = 180 - 75 - 45 = 60°
2) Сумма двух острых углов прямоугольного треугольника равна 90° ⇒ ∠B = 90 - 60 = 30°; катет, лежащий напротив угла в 30°, равен половине гипотенузы ⇒ AB = 2 * AC = 2 * 3 = 6 см
5.1) Рассмотрим Δ ABD
∠A + ∠B = 90° (как острые углы в прямоугольном Δ) ⇒ ∠A = 90 - 45 = 45°; ∠A = ∠B ⇒ Δ ABD - р/б ⇒ BD = AD = 5 см
Рассмотрим Δ BCD
Катет CD = 7 ÷ 2 = 3,5 см (т. к. лежит напротив угла в 30°)
AC = AD + CD = 5 + 3,5 = 8,5 см
9
Объяснение:
Рассмотрим тр-к АВС:
угол В = 180-угА-угС=180-90-30=60
МВ-биссектриса, значит угМВС=угВ : 2=60:2=30
Рассмотрим тр-к МВС:
Гипотенуза МВ=6 (по усл)
МС - катет противолежащий углу 30
значит МС=МВ : 2=6:2=3 (по св-ву прямоугольного тр-ка с углом 30)
дополнительно проведем высоту MN на сторону АВ и рассмотрим тр-к MNB:
угNBM=угMBC=30
Гипотенуза МВ=6 (по усл)
катет MN=МВ : 2=6:2=3 (по св-ву прямоугольного тр-ка с углом 30)
Рассмотрим тр-к AMN
угА=30 (по усл)
Гипотенуза АM=МN*2=3*2=6 (по св-ву прямоугольного тр-ка с углом 30)
Имеем
АС=АМ+МС=6+3=9
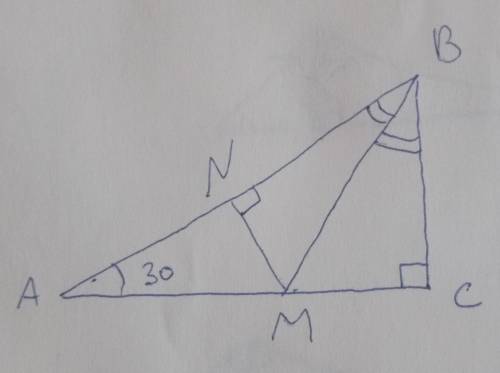
ответ: решение на фото
Объяснение: