∠SAO = 60°
Объяснение:
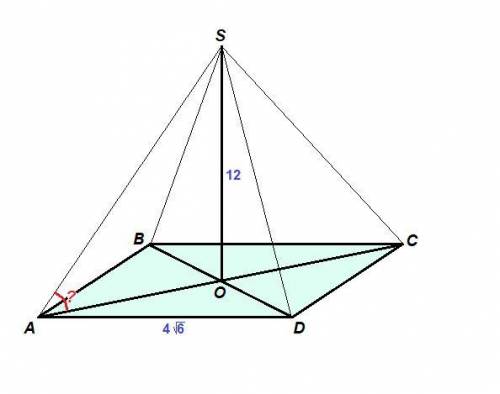
Проведем SO⊥(ABC).
SO = 12 см - расстояние от S до плоскости квадрата.
Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на плоскость.АО - проекция SA на (АВС), значит
∠SAO - угол между прямой SA и плоскостью квадрата - искомый.
SA = SB = SC = SD по условию.
Если равны наклонные, проведенные к плоскости из одной точки, то равны и их проекции:OA = OB = OC = OD.
Значит, О - центр квадрата (точка пересечения диагоналей).
AD = 4√6 см, тогда диагональ квадрата:
AC = AD√2 = 4√6 · √2 = 8√3 см
AO = 0,5 AC = 0,5 · 8√3 = 4√3 см
Из прямоугольного треугольника SOA:
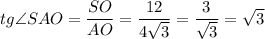
∠SAO = 60°
Пусть лдин угол Х°, то другой (Х+112)°
х+х+112=180
2х=180-112
2х=68
х=68:2
х=34° первый угол
34+112=146° второй угол
ответ: 34°;146°.