Дан параллелограмм ABCD На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что АМ = CN Докажите, что MBND –
Доказываешь, что два треугольник AMD и CNB:АМ = CN по условию,АВ=СВ, т.к. это стороны параллелограмма.По первому признаку равенства треугольников: AMD = CNBИз того же равенства треугольников получаешь, чтоПроверенные ответы содержат наджную, заслуживающую доверия информацию, оценнную командой экспертов. На «Знаниях» вы найдте миллионы ответов, правильность которых подтвердили активные участники сообщества, но Проверенные ответы — это лучшие из лучших.Диагональ ВD исходного параллелограмма АВСD осталась прежней, диагональACс каждой стороны увеличилась на одинаковую длину. Точка пересечения диагонали ВD и диагоналиМNосталась прежней и делит их, как и в исходном четырехугольнике, пополам.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник параллелограмм.
DE – радиус данной окружности.
Возьмём точку К (4;-7), проведем по линиям клеток DK и EK.
DK=|-5–(-7)|=|-5+7|=2
EK=|4–(-2)|=|4+2|=6
Так как углы любой клетки равны 90°, то угол DKE=90°.
Тогда по теореме Пифагора в ∆DKE:
DE²=DK²+EK²
DE²=2²+6²
DE²=4+36
DE²=40
То есть квадрат радиуса окружности равен 40.
Уравнение окружности имеет вид:
(x–a)²+(y–b)²=R²
где кординаты центра окружности (а;b), а R – радиус.
a) Центр окружности – точка D имеет кординаты (4;-5), тогда получим уравнение:
(x–4)²+(y+5)²=40
b) Центр окружности – точка E имеет кординаты (-2;-7), получим уравнение:
(х+2)²+(у+7)²=40
ответ выделен жирным шрифтом. Так как не дано какая из двух точек центр, я расписал два случая. Но вероятнее что всё-таки случай а)
Тогда ответ: (x–4)²+(y+5)²=40
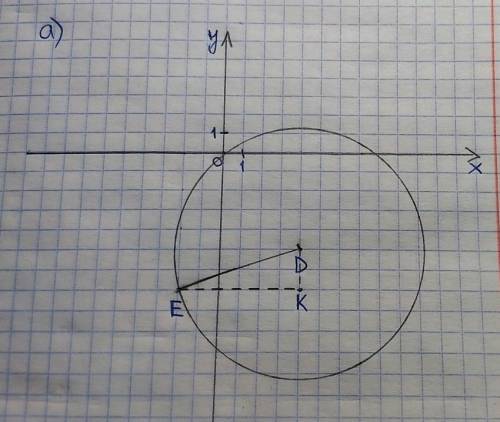
У ромба все стороны равны.Если АД-это сторона ромба,то Р=4*14=56
Если АД-диагональ,то Р=56*√3/3