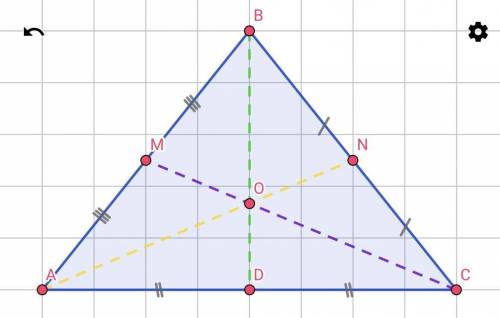
△ABC - равнобедренный;
AB = BC;
BD = 160 (см), AC = 80 (см);
BD, AN, CM - медианы;
Найти:AN = ? (см); CM = ? (см).
Решение:"Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2 : 1, считая от вершины".
⇒ NO : AO = DO : BO = MO : CO = 1 : 2.
BO = 2/3 ⋅ BD = 2/3 ⋅ 160 = 320/3 (см).
DO = 1/3 ⋅ BD = 1/3 ⋅ 160 = 160/3 (см).
Поскольку отрезок BD - медиана ⇒ AD = DC = 80 ⋅ 1/2 = 80/2 = 40 (см).
Т.к. △ABC - равнобедренный ⇒ AO = OC (это равенство также можно обосновать тем, что прямоугольные треугольники AOD и COD равны, по двум катетам: AD = DC по свойству медианы BD, OD - общий катет).
Найдём АО и OC, по теореме Пифагора (c = √(a² + b²), где c - гипотенуза, a и b - катеты).
AO = √(DO² + AD²) = √((160/3)² + 40²) = 200/3 (см).
OC = √(DO² + DC²) = √((160/3)² + 40²) = 200/3 (см).
AO = 2/3 ⋅ AN, по свойству медиан треугольника.
Составим и решим уравнение (AN - x (см)):
2/3 ⋅ x = 200/3
x = 200/3 : 2/3
x = 200/3 ⋅ 3/2
x = 100
100 (см) - величина медианы AN.
Поскольку △ABC - равнобедренный ⇒ AN = CM = 100 (см).
ответ: 100 (см), 100 (см).