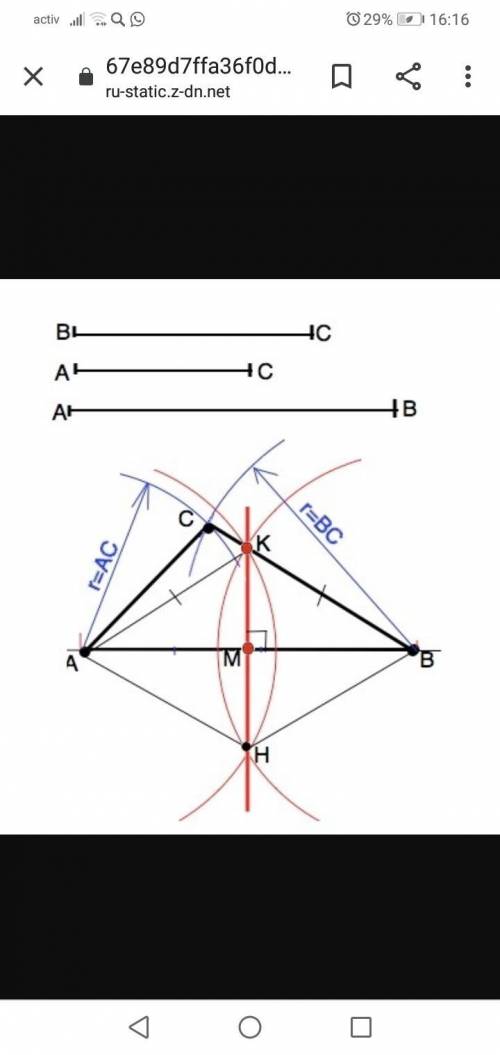
ответ:. На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг - вершина С искомого треугольника.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса, но больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
Объяснение: делал на скорую руку
одна сторона квадрата h=b=24 - это высота призмы
смежная с ней сторона квадрата P=b=24 - это периметр основания
высота одна и та же h=b=24 - это высота призмы
в правильной треугольной призмы -
сторона основания a=P/3=b/3=24/3=8 см
площадь основания S∆= a^2√3/2=8^2√3/2=64√3/2=32√3 см2
объем призмы V∆=S∆*h=32√3h
в правильной четырехугольной призмы -
сторона основания c=P/4=b/4=24/4=6 см
площадь основания S□= c^2=6^2=36 см2
объем призмы V□=S□*h=36h
V∆ /V□ =32√3h /36h =8√3 / 9 =8√3 : 9
ОТВЕТ V∆ /V□ = 8√3 / 9 =8√3 : 9
Разница а расстояний концов отрезка от плоскости равна
а = 0.5 - 0,3 = 0,2(м).
этой разнице а соответствует 10 частей, а разнице расстояний х до плоскости между точкой деления и менее удалённым от плоскости концом отрезка точки соответствуют 3 части , тогда х равен
х = 0,2 · 3 : 10 = 0,06(м)
Полное расстояние от точки деления отрезка до плоскости равно:
0,3 + 0,06 = 0,36(м)
ответ: 0,36м