классно это "больше меньше" пусть будет просто "больше", с "меньше" и с "больше меньше" тогда сами, плз :)))
пусть полугла С = x, тогда А = 6х, В = 3х; С=2х(само собой)
А+В+С = 180; 11х = 180; х = 180/11, А = 1080/11. Ну, за что продал.
а что будет с "меньше"?
B = y, A = 2y, C = 6y тут числа выходять целые.
y = 20, А = 40..
случай "больше меньше" решать не буду :
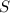 ,
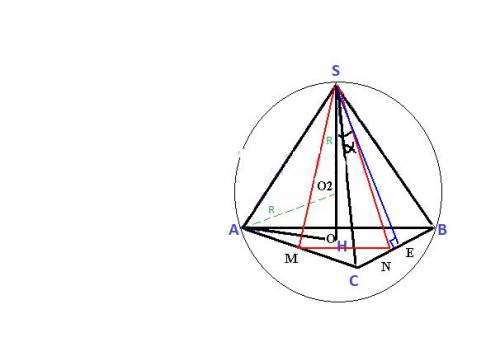
, 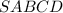 правильная пирамида .
правильная пирамида .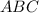 правильный треугольник , тогда обозначим
правильный треугольник , тогда обозначим 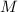 -середину стороны
-середину стороны 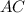 .
. 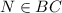
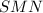 .
. 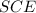 равен
равен 
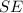 - апофема.
- апофема. 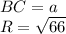
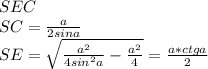
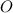 центра вписанной окружности в основание
центра вписанной окружности в основание 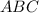 , тогда по формуле
, тогда по формуле 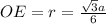
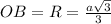 .
. совпадает с центром вписанной окружности
совпадает с центром вписанной окружности 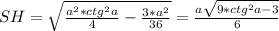
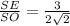
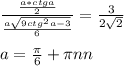
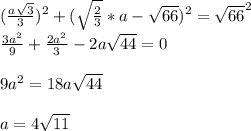
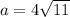
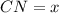
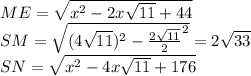
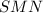 по теореме косинусов , затем выражая синус через косинус получим
по теореме косинусов , затем выражая синус через косинус получим 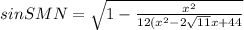
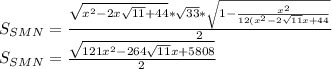
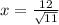
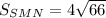
A=2B
C=3A=6B
B+2B+6B=9B=180 B=20
A=40
ответ 40 градусов