SO=5√2см
S(∆SAC)=50см²
S(ABCD)=100см²
Объяснение:
Дано:
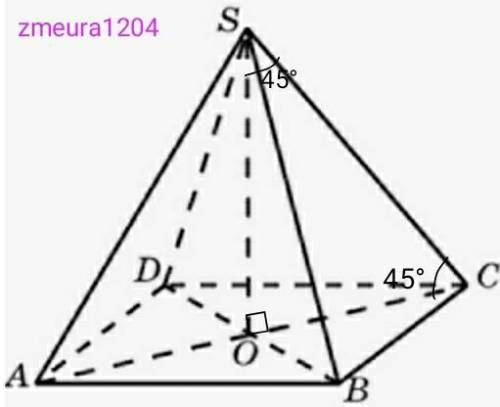
SABCD- пирамида.
ABCD- квадрат.
SC=SB=SA=SD=10см.
<SCO=45°
SO=?
S(∆SAC)=?
S(ABCD)=?
Решение
Рассмотрим треугольник ∆SOC
<SOC=90°; <SCO=45°; <OSC=45°.
Треугольник ∆SOC- прямоугольный, равнобедренный. SO=OC.
Пусть ОС будет х см, тогда SO тоже будет х см.
По теореме Пифагора SC²=SO²+OC², составляем уравнение.
х²+х²=10²
2х²=100
х=√50
х=5√2 см SO и ОС (высота пирамиды и половина диагонали квадрата).
SO=5√2 см.
АС=2*ОС=2*5√2=10√2 см.
S(∆SAC)=1/2*AC*SO=1/2*10√2*5√2=50см² площадь диагонального сечения.
AB=AC/√2=10√2/√2=10см сторона квадрата.
S(ABCD)=AB²=10²=100см²
Как известно, диагонали точкой пересечения делятся пополам, а противоаоложные стороны пар-мма равны. Следовательно, противоположные по отношению друг к другу треугольники равны(по 3-ему признаку равенства треугольников), и площади их тоже равны.
Осталось доказать, что площади двух "смежных" треугольников равны. Рассмотрим их. Одна сторона у них общая, примем за основание сторону, лежащую на диагонали. Эти стороны у треугольников равны, т.к. точкой пересечения, повторюсь, диагонали делятся пополам. Прощадь треугольника у нас равна половине основания, умноженного на высоту, проведенную к основанию. Проведи к основаниям треугольников высоту - это будет один и тот же отрезок.
Мы получили - основания у треугольников равны, высоты равны.
Теорема доказана.
Следовательно, двугранный угол при основании пирамиды равен линейному углу между высотой грани и ее проекцией на основание. Эта проекция - отрезок, соединяющий точку О, в которую проецируется высота пирамиды на основание пирамиды. Раз все двугранные углы равны, значит равны и эти отрезки и мы доказали пункт б).
Равенство этих проекций доказывает, что точка О равноудалена от сторон треугольника. Это значит, что точка О - центр вписанной окружности в основание треугольника, то есть доказан пункт а).
Найдем длину проекции на плоскость основания высот боковых граней, проведенных из вершины пирамиды, или, как мы доказали, радиус вписанной в основание пирамиды окружности.
В равнобедренном треугольнике АВС BН - его высота, АН=НС=а/2.
Тогда АВ=АН/Cosα или AB=a/(2Cosα). BH=AB*Sinα или BH=a*Sinα/(2Cosα)=(а/2)*tgα.
Sabc=(1/2)*AC*BH или Sabc=(а/2)*(а/2)*tgα=(а²/4)*tgα.
Есть формула площади треугольника: S=p*r, где р - полупериметр,
r - радиус вписанной окружности. Тогда r=S/p или r=[(а²/4)*tgα]/p. p=2*AB+AC. Или
р=2*a/(2Cosα)+а=a/Cosα+а=а((1/Cosα)+1)=(а*(1+Cosα))/Cosα.
r=[(а²/4)*tgα]/[(а*(1+Cosα))/Cosα] или r=a*Sinα/[4(1+Cosα)].
ответ: r=a*Sinα/[4(1+Cosα)].