Прямые параллельны
∠ TKM
Объяснение:
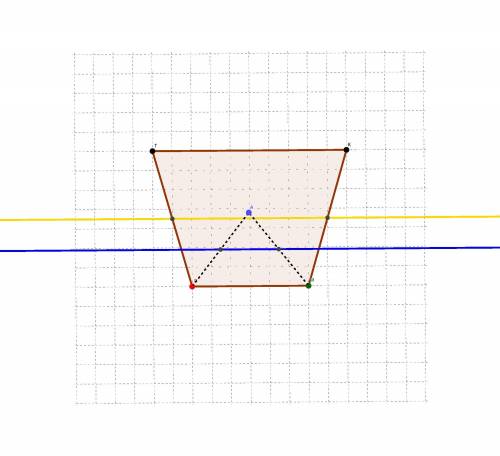
Прямая, содержащая середины отрезков OM и OP (буду называть ее а) также содержит среднюю линию треугольника OMP, соответственно прямая a параллельна MP.
Средняя линия трапеции параллельна основаниям трапеции (в частности MP). Следовательно прямая, содержащая среднюю линию трапеции (буду называть b) параллельна MP.
Прямые a и b параллельны MP следовательно они параллельны между собой.
Угол между a и MK равен углу между b и MK , TK и MK т.е ∠ TKM и т.д
Т.к никаких конкретных данных по трапеции не дано, найти числовое значение этого угла не представляется возможным
ꟷꟷꟷꟷꟷꟷ
Не забывайте сказать " "! и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
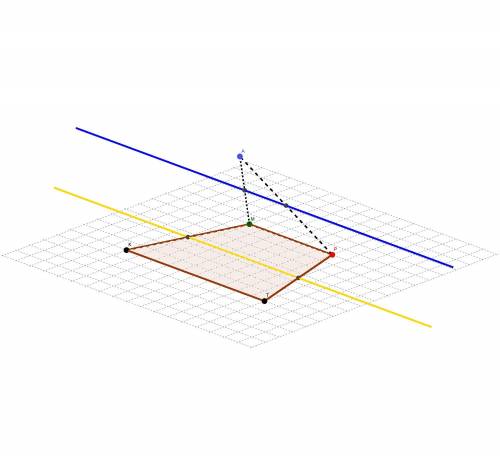
Даны координаты вершин пирамиды А1А2А3А4. АВСD :
А1(4;3;6), А2(4;9;4), А3(5;10;3), А4(3;1;3).
Для удобства назовём их АВСD.
А(4;3;6), B(4;9;4), C(5;10;3), D(3;1;3).
а)Найдите угол между ребром А1А4 (AD) и гранью А1А2А3 (ABC).
Находим векторы АВ и АС.
АВ = (0; 6; -2), АС = (1; 7; -3).
Их векторное произведение равно.
i j k | i j
0 6 -2 | 0 6
1 7 -3 | 1 7 = -18i - 2j + 0k - 0j + 14i - 6k = -4i - 2j - 6k.
Нормальный вектор к плоскости АВС равен (-4; -2; -6).
Модуль равен √((-4)²+ (-2)² + (-6)²) = √(16 + 4 + 36) = √56 ≈
7,483.
Вектор АD
x y z Модуль
-1 -2 -3 √14 ≈ 3,74166
.
cos α = (-1*(-4) + (-2)*(-2) + (-3)*(-6))/(√14*√56) =
= (4 + 4 + 18)/(√14*2√14) = 26/28 =
13/14 ≈ 0,9286.
α = 0,38025 радиан или 21,7868 градуса
.
б)Уравнение высоты, опущенной из вершины А4 (D) на грань А1А2А3 (ABC).
Её направляющий вектор найден - он равен нормальному вектору плоскости АВС(-4; -2; -6).
Используем координаты точки D(3; 1; 3).
Уравнение высоты DH: (x – 3)/(-4) = (y – 1)/(-2) = (z – 3)/(-6).
В правильной треугольной пирамиде проекция бокового ребра L на основание равна (2/3) высоты основания h.
(2/3)h = L*cos 30° = 6*(√3/2) = 3√3 см.
h = (3√3)*(3/2) = 9√3/2.
Отсюда находим сторону а основания из выражения:
h = a√3/2.
Тогда а = 2h/√3 = (2*(9√3/2))*/√3 = 9 см.
Площадь основания So = a²√3/4 = 81√3/4.
Находим апофему А:
А = √(L² - (a/2)²) = √(36 - (9/2)²) = √(36 - (81/4)) = √63/2.
Периметр основания Р = 3а = 3*9 = 27 см.
Находим площадь боковой поверхности.
Sбок = (1/2)РА = (1/2)*27*(√63/2) = 27√63/4 см².
Полная площадь поверхности пирамиды равна:
S = So + Sбок = (81√3/4) + (27√63/4) = (27/4)(3√3 + √63).
Высота H пирамиды равна: H = L*sin 30° = 6*(1/2) = 3 см.
Тогда объём пирамиды равен:
V = (1/3)SoH = (1/3)*(81√3/4)*3 = (81√3/4) см³.