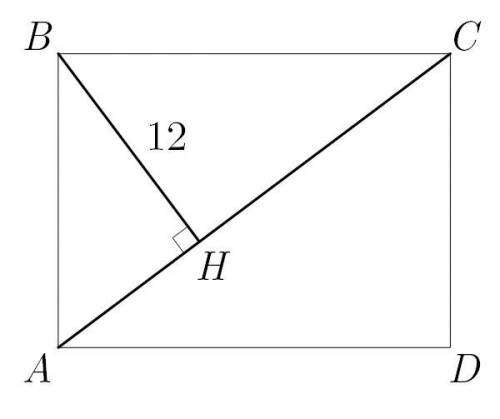
Площадь прямоугольника равна 300 см2.
Объяснение:
Так как периметр прямоугольника равен 70, то сумма смежных сторон равна 35.
Пусть  ,
, 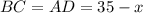 ;
; 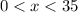 .
.
Тогда по теореме Пифагора из треугольника 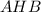
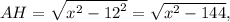
а из треугольника 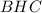
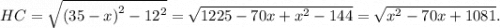
Так как 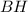 — высота прямоугольного треугольника, проведенная к гипотенузе, ее можно выразить по формуле
— высота прямоугольного треугольника, проведенная к гипотенузе, ее можно выразить по формуле
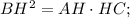
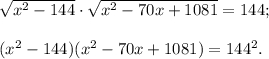
Разложим каждый из трехчленов на множители. Для первого это легко сделать по формуле разности квадратов
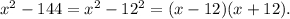
Корни второго найдем через дискриминант:
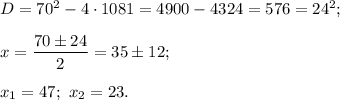
Тогда по формуле
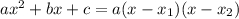
получаем, что
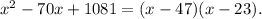
Значит уравнение перепишется в таком виде:
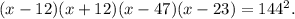
Перегруппируем сомножители:
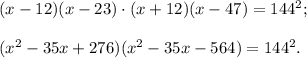
Сделаем замену 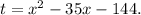
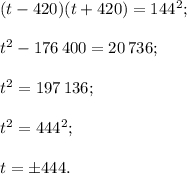
Делая обратную замену, получаем два случая.
1) 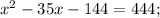
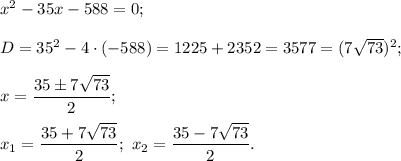
Оценим второй получившийся корень:
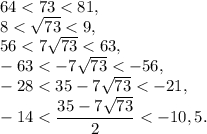
Получили  , что противоречит смыслу задачи, следовательно,
, что противоречит смыслу задачи, следовательно, 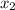 — посторонний корень.
— посторонний корень.
Аналогично
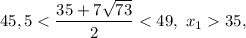
значит корень 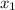 также посторонний.
также посторонний.
2) 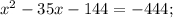
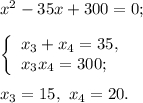
Оба этих корня подходят: при 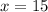 значение
значение 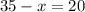 и наоборот.
и наоборот.
Таким образом, площадь прямоугольника 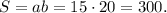
30.51
1. Г
2. Д
3, В
30.52
1. Б
2. В
3, Д
Объяснение:
30.51
Зная три стороны треугольника можно найти его площадь по формуле Герона:
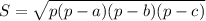
где р - полупериметр треугольника,
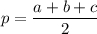
Затем можно найти радиус вписанной окружности по формуле:
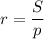
1. а = 5 см, b = 6 см, с = 7 см.
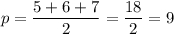 см
см
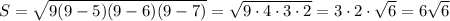 см²
см²
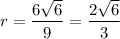 см
см
ответ: Г.
2. а = 4 см, b = 6 см, с = 8 см.
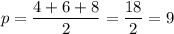 см
см
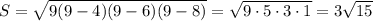 см²
см²
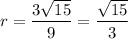 см
см
ответ: Д.
3. а = 12 см, b = 16 см, с = 20 см.
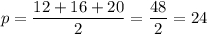 см
см
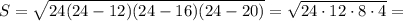
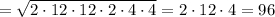 см²
см²
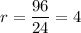 см
см
ответ: В.
30.52
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.1. S₁ : S₂ = 100, ⇒ k² = 100
k = 10
ответ: Б.
2. S₁ : S₂ = 64, ⇒ k² = 64
k = 8
ответ: В.
3. S₁ : S₂ = 25, ⇒ k² = 25
k = 5
ответ: Д.
a-b=2 по усл.
а=2+b
(2+b)*b=48
b^2+2b=48
По Т Виета:
b1+b2=-2
b1*b2=48
b1=-8 (не удвл, т.к отриц.)
b2=6
b=6
a=6+2=8
По Т Пифагора:
d^2=R^2=a^2+b^2
R^2=64+36=100
R=10