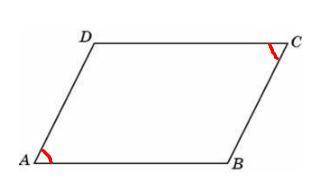
Один угол параллелограмма больше другого на 78 градусов. Найдите больший угол ответ дайте в градусах.
По признаку параллелограмма - противоположные углы параллелограмма одинаковые. Значит:
∠DAB = ∠DCB и ∠ADC = ∠CDA.
Пользуясь еще одним важным свойством параллелограмма - сумма углов параллелограмма прилегающих к любой стороне равна 180° - составим уравнение.
Пусть меньший угол параллелограмма - x градусов. Тогда больший - (x+78) градусов. Так как их сумма 180° имеем:
x + x + 78 = 180
2x = 180 - 78
2x = 102
x = 102 : 2
x = 51
Таким образом меньший угол фигуры равен 51°.
Тогда больший: 51 + 78 = 129°
ответ: 129°
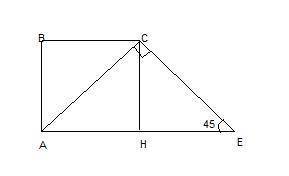
Вариант 1. По теореме о касательной (РС) и секущей (2АС+ВС):
РВ² = (60+60+15)*15.
РВ = √(135*15) = 45 ед.
Вариант 2. Треугольник АРВ прямоугольный (<Р=90°), так как радиус перпендикулярен касательной в точке касания. Тогда по Пифагору:
РВ = √(АВ²- АР²) = √(75²-60²) = √(15*135) =45 ед.