Высоту, опущенную на основание найдем по теореме Пифагора
h=√(7²-2²)=3√5см
Площадь равна половине произведения высоты на основание:
S=1/2(3√5*4)=6√5см²
ответ: 6√5см²
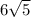 см².
см².
Объяснение:
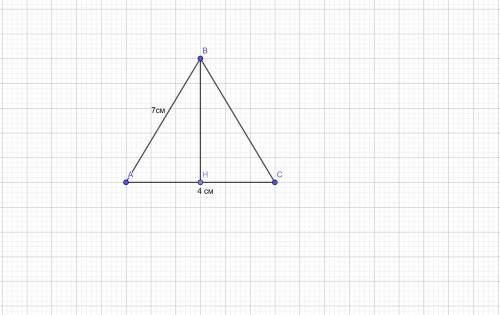
ΔABC - равнобедренный
AB=BC = 7 см; AC=4 см.
Проведем высоту BH. В равнобедренном треугольнике высота, проведенная к основанию , является медианой. ЗначитAH=HC= 2 см. Рассмотрим ΔAHB - прямоугольный. Найдем высоту BH треугольника по теореме Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
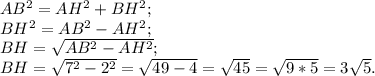
Площадь треугольника найдем по формуле :
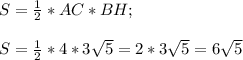
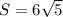 см.²
см.²
Найдем площадь по формуле Герона :
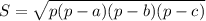 , где a,b,c - стороны треугольника , p - полупериметр
, где a,b,c - стороны треугольника , p - полупериметр
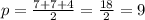 см.
см.
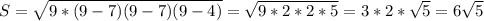 см².
см².
Объяснение:
4)
Уравнение окружности (x – х₀)²+ (y – у₀)² = R² , (х₀ ; у₀)-координаты центра.В(3;-2)-центр, А(-1;-4) принадлежит окружности. Найдем R.
R²=АВ²= (3+1)²+(-2+4)² =4²+2²=20.
(x – 3)²+ (y +2)² =20.
5)
MN-диаметр , M(-2;1) , N(4;-5). Пусть О-середина MN , найдем координаты О.
х(О)= ( х(M)+х(N) )/2 у(О)= ( у(M)+у(N) )/2
х(О)= ( -2+4 )/2 у(О)= ( 1-5 )/2
х(О)= 11 у(О)= -2
О( 1 ;-2) .
R²=ОN²= (4+1)²+(-5+2)² =25+9=34.
(x – 1 )²+ (y +2)² =34.
4.
Общее уравнение окружности с центром в точке (а; b) и радиусом R выглядит так (х-а)²+(у-b)²=R²
Центр есть, радиуса нет. для того, чтобы найти радиус, подставим вместо х и у координаты точки А, и координаты центра - точки В
(-1-3)²+(-4+2)²=R²⇒=R²=16+4=20, радиус равен √20=2√5
Искомое уравнение (х-3)²+(у+2)²=(2√5)²
или (х-3)²+(у+2)²=20
5 Найдем центр окружности, это середина диаметра
а=(-2+4)/2=1
b=(1-5)/2=-2
Центр (1;-2)
Найдем длину диаметра по ее координатам, а потом радиус, поделив длину на два.
√((4+2)²+(-5-1)²)=√(36+36)=6√2
значит, R²= (3√2)²=18
или так МО= √((1+2)²+(-2-1)²)=√18=3√2
искомое уравнение имеет вид
(х-1)²+(у+2)²=18
6√5 см²
Объяснение:
Пусть дан Δ ABC (AB = BC=7см) AC = 4 см, BB₁ - высота, тогда BB₁ - медиана (свойство равнобедренного треугольника) ⇒ B₁C = 2 см
Находим BB₁ из ΔBB₁C (∠B₁ = 90°) по теореме Пифагора:
BB₁² = BC² - B₁C² = 7² - 2² = 45 ⇒ BB₁ = 3√5 см
SΔABC = 1/2 · AC · BB₁ = B₁C · BB₁ = 2 · 3√5 = 6√5 см²