а) СХ = 1,75 см; XD = 5,25 см;
б) ∠АХС = 116°
Объяснение:
Смотри прикреплённый рисунок.
а)
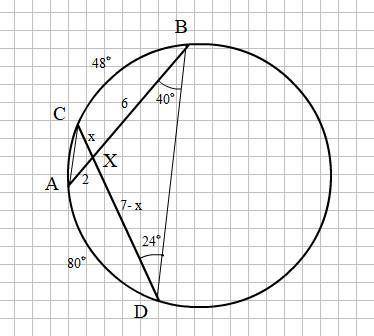
∠САВ = ∠СDB = 24° так как опираются на одну и ту же дугу ВС = 48°
∠АСD = ∠ABD = 40° так как опираются на одну и ту же дугу AD = 80°
ΔACX ~ ΔDBX по двум равным углам.
Пусть СХ = x, тогда XD = 7 - x
Следовательно, AX : XB = CX : XD
2 : 6 = x : (7 - x)
2( 7 - x) = 6x
14 - 2x = 6x
8x = 14
x = 1.75 (см) - это CX
7 - x = 7 - 1.75 = 5.25 (cм) - это XD
б)
В Δ САХ известны два угла
∠САХ = ∠САВ = 24°; ∠АСХ = ∠АСD = 40°
Согласно свойству углов треугольника
∠АХС = 180 ° - (∠САХ + ∠АСХ) = 180° - (24° + 40°) = 116°
а) СХ = 1,75 см; XD = 5,25 см;
б) ∠АХС = 116°
Объяснение:
Смотри прикреплённый рисунок.
а)
∠САВ = ∠СDB = 24° так как опираются на одну и ту же дугу ВС = 48°
∠АСD = ∠ABD = 40° так как опираются на одну и ту же дугу AD = 80°
ΔACX ~ ΔDBX по двум равным углам.
Пусть СХ = x, тогда XD = 7 - x
Следовательно, AX : XB = CX : XD
2 : 6 = x : (7 - x)
2( 7 - x) = 6x
14 - 2x = 6x
8x = 14
x = 1.75 (см) - это CX
7 - x = 7 - 1.75 = 5.25 (cм) - это XD
б)
В Δ САХ известны два угла
∠САХ = ∠САВ = 24°; ∠АСХ = ∠АСD = 40°
Согласно свойству углов треугольника
∠АХС = 180 ° - (∠САХ + ∠АСХ) = 180° - (24° + 40°) = 116°

Объяснение:
Рисунок к задаче в приложении.
Построить три заданных точки не очень трудно.
А вот четвёртую точку - С - построим силой Разума.
мысль 1 - стороны параллелограмма параллельны
мысль 2 - противоположные стороны равны - AD = BC.
мысль 3 - как точка D сдвинута от точки А, так и точка С сдвинута от точки В.
РЕШЕНИЕ
Вычисляем разность координат точек А и D.
dX = Dx - Ax = -2 - (-3) = +1 - сдвинута на 1 вправо.
dY = Dy - Ay = -5 - (-2) = - 3 - сдвинута на 3 вниз.
Такие же сдвигу применим к точке В и получим координату точки С.
Cx= Bx + 1 = 4 + 1 = 5
Cy = By - 3 = 7 - 3 = 4
ОТВЕТ: С(5;4) - координата точки С.