1)
Объяснение:
1) Все диаметры окружности равны между собой.
Верно.
Диаметр в два раза больше радиуса, а все радиусы окружности равны.
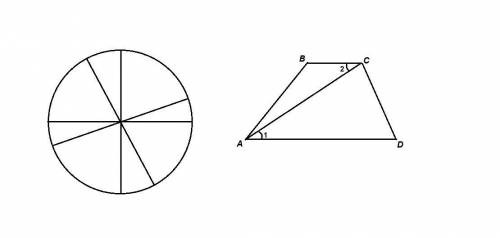
2) Диагональ трапеции делит ее на два равных треугольника.
Неверно.
Диагональ параллелограмма делит его на два равных треугольника, в трапеции эти треугольники очевидно не равны:
для ΔАВС и ΔADC АС - общая сторона, ∠1 = ∠2 как накрест лежащие при пересечении AD║ВС и секущей АС, но AD ≠ ВС.
3) Площадь любого параллелограмма равна произведению длин его сторон.
Неверно.
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
АВ/А1В1=AB/40 (2/5=AB/40, AB=(40*2)/5, AB=16)
AC/A1C1=AC/28 (2/5=AC/28, AC=(28*2)/5, AC=11,2)