Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей и равна ее половине.
Прямая верна.
Обратно.
Если отрезок параллелен стороне треугольника и соединяет стороны двух других сторон, то он является средней линией треугольника. Но это уже получается определение средней линии и на практике обратной теоремой не пользуемся.
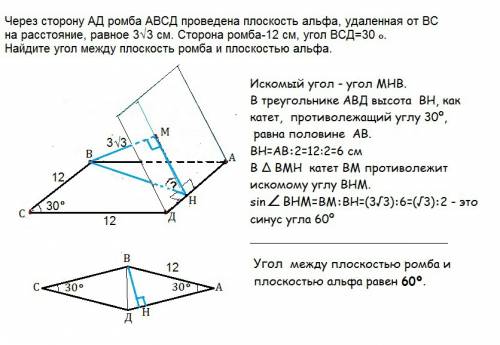
Через сторону АД ромба АВСД проведена плоскость альфа, удаленная от ВС на расстояние, равное 3√ 3 см. Сторона ромба-12 см, угол ВСД=30º. Найдите угол между плоскость ромба и плоскостью альфа
ВС ║АД, ⇒ ВС║α
АД ∈ плоскости α, и расстояние от ВС до плоскости равно длине отрезка их общего перпендикуляра (свойство).
Угол между плоскость ромба и плоскостью α -двугранный угол, и его величина определяется градусной мерой линейного угла.
В данном случае это величина угла, который получится, если из точки Н к АД— линии пересечения плоскости ромба и плоскости альфа, —провести перпендикуляры в обеих плоскостях.
Пусть Н - основание высоты ромба, проведенной из В к АД, а НМ перпендикуляр к АД в плоскости альфа. (см. рисунок)
Искомый угол - угол МНВ.
В треугольнике АВД высота ВН как катет, противолежащий углу 30º, равна половине гипотенузы АВ.
ВН=АВ:2=12:2=6 см
В ∆ ВМН катет ВМ противолежит искомому углу ВНМ.
sin∠ВНМ=ВМ:ВН=(3√3):6=(√3):2 - это синус угла 60º
Угол между плоскость ромба и плоскостью альфа равен 60º.
2 задача. Найдем диагональ прямоугольника со сторонами 4 и 6 см. По скольку, согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов
42 + 62 = 16+36=корень 52=7,21 Сравним полученный её с известной диагональю параллелограмма 8 — 7,21 = 0,29 По скольку известная диагональ больше диагонали прямоугольника, то , как было сказано выше, необходимо полученную разницу вычесть из величины диагонали прямоугольника, чтобы получить меньшую, искомую, диагональ.
И так: 7,21 — 0,29 = 6,92 см.
3 задача.
R=a/2sin60
а=R*2*sin60=9*2*(корень из 3)/2=9*корень из3
Есть теорема Сумма смежных углов равна 180 градусов
Обратная теорема. Если сумма углов равна 180 градусов , то они смежные.
Почему это не так? Взять например квадрат, и его противоположные углы, их сумма 90+90=180 градусов, но они не смежные
Напр. Теорема. Вертикальные углы равны
Обратная. Если углы равны, то они вертикальные.
Это не так. Возьмем напр. опять квадрат и его противоположные углы, они равны (каждый по 90 градусов), но не являются вертикальными
Подробнее - на -