Объяснение:
ЗАДАЧА 70
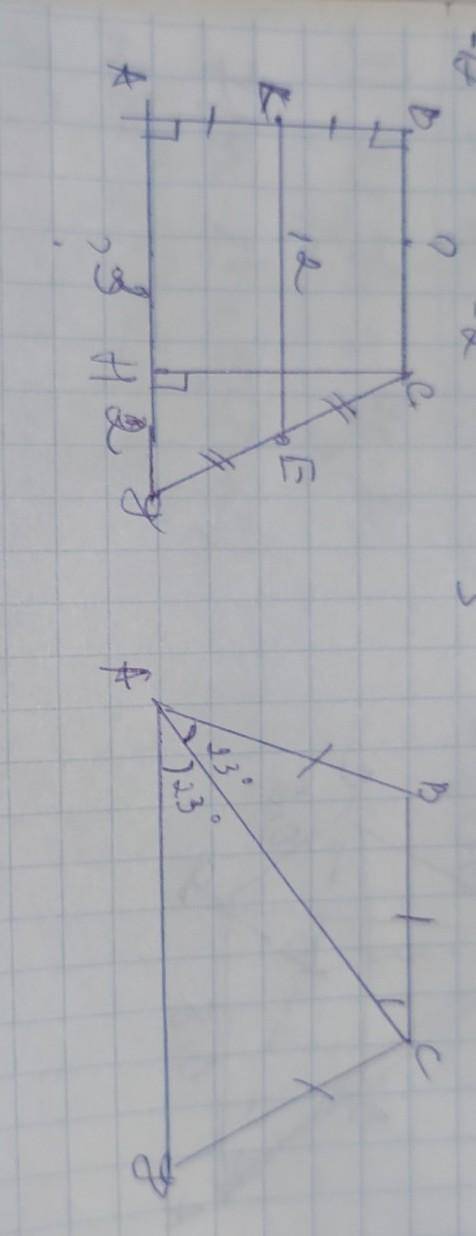
обозначим вершины трапеции А В С Д с высотой СН, с основаниями ВС и АД и средней линией КЕ.
СН делит основании АД:
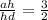
обозначим эти пропорции как 3х и 2х. СН делит АД так, что АН=ВС=3х. Составим уравнение используя формулу нахождения средней линии трапеции:
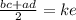
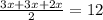
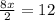
4х=12
х=12÷4=3
тогда ВС=3×3=9см, АД=3х+2х=5х=5×3=15см
ОТВЕТ: ВС=9см, АД=15см
ЗАДАЧА 71
Обозначим вершины трапеции А В С Д с основаниями ВС и АД и диагональю АС. Рассмотрим ∆АВС. Если АВ=ВС, то ∆АВС - равнобедренный, поэтому <ВАС=<ВСА, а также <ВСА=<САД как внутренние разносторонние, поэтому диагональ АС является биссектрисой угла А, значит угол А=23×2=46°. Сумма углов трапеции прилегающих к одной боковой стороне составляют 180°, поэтому <В=<С=180–46=134°. Так как трапеция равнобедренная то <А=<Д=46°, <В=<С=134°
ОТВЕТ: 46°, 134°
Вершины треугольника делят описанную около него окружность на три дуги длины которых относятся как 2:7:9. Найди радиус окружности если больше из сторон равна 30.
Объяснение:
В треугольнике больший угол лежит против большей дуги в 9 частей . И значит эта дуга стягивает наибольшую сторону в 30 ед.
Пусть одна часть х° , тогда градусная мера дуг составляющих окружность будет : 2х, 7х, 9х.
2х+7х+9х=360° , х=20° . Большая из дуг 9*20°=180° ⇒ эта дуга половина окружности ⇒ она стягивает диаметр .
Значит r=30:2=15 (ед).