Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:
S=
=2(5 умножить на 1 плюс 7 умножить на 1 плюс 7 умножить на 5) плюс 2(1 умножить на 1 плюс 2 умножить на 1 плюс 2 умножить на 1) минус 4(2 умножить на 1)=
=96.
ответ: 96.
Объяснение:
9/12 ₽/'1₽!'08#!'0=#!#standoff2' #09'! ##'
Основание треугольника равно 15 см
Объяснение:
Дано:
Смотри прикреплённый рисунок.
ΔАВС - равнобедренный:
АВ = ВС и АС - основание
∠ВАС = ∠АСВ
∠АВС = 0,5 ∠ВАС
АМ - биссектриса
Найти:
Основание АС
Пусть ∠ВАС = ∠ВСА = 2х, тогда ∠АВС = х
Биссектриса АМ делит ∠ВАС пополам, значит
∠ВАМ = 0,5 ∠ВАС = 0,5 · 2х = х.
В Δ АВМ: ∠АВМ = ∠АВС = х.
Δ АВМ - равнобедренный, так как ∠ВАМ = ∠АВМ = х
∠АМС является внешним углом при вершине М для ΔАВМ, поэтому
∠АМС = ∠АВМ + ∠ВАМ = х + х = 2х
Δ АМС - равнобедренный, так как ∠АМС = 2х и ∠АСМ = ∠АСВ = 2х
Тогда АС = АМ = 15 см.
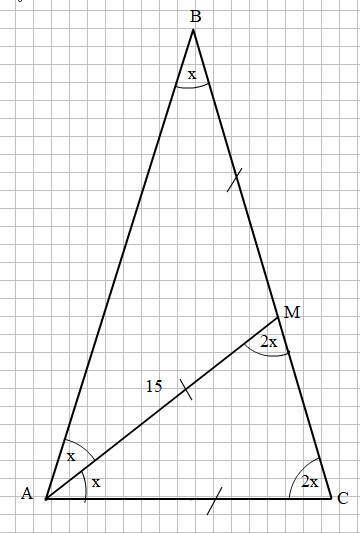
Треугольник АВС
АС = 20 см.
АВ = 15 см.
ВС - гипотенуза
АН - медиана
Найти - АН.
Решение:
По теореме Пифагора находим ВС:
ВС = 25 см.
Медиана, проведённая из угла 90° равна половине гипотенузе, находим АН:
АН = ВС : 2 = 25см. : 2 = 12,5 см.
ответ: 12,5 см.