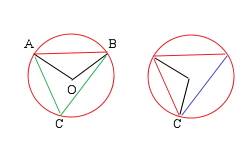
Прямая, проведенная из конца стороны-диаметра в точку пересечения окружности с противоположной боковой стороной, перпендикулярна это стороне, потому что вписанный угол, опирающийся на диаметр, равен 90 градусам. Поэтому эта прямая образует с основанием угол в 90 - 60 = 30 градусов. Соответственно, дуга, на которую этот угол опирается, равна 60 градусам. Само собой, это верно и для второй боковой стороны. Поэтому полуокружность делится сторонами равностороннего треугольника, построенного на диаметре, на три равные дуги по 60 градусов каждая.
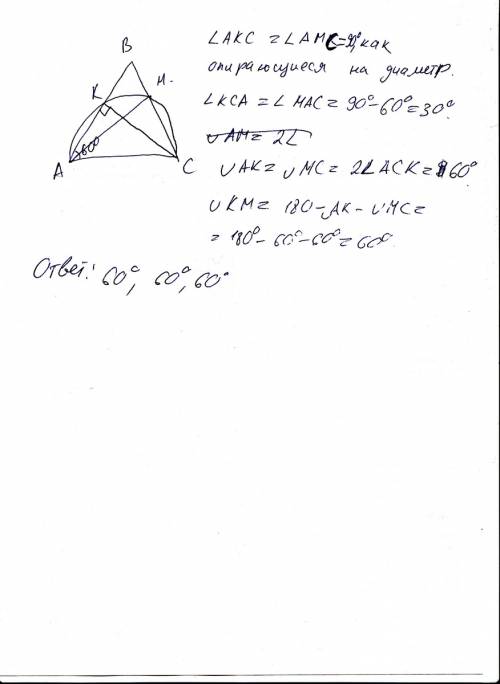
если сказано, что сторона (АВ) видна из центра под углом 100 градусов, это значит,
что задан центральный угол (АОВ) и он равен 100 градусов и тем самым задан угол
вписанного треугольника, лежащий против стороны АВ --- угол АСВ
этот угол вписанный, т.е. он равен половине центрального, опирающегося на ту же дугу,
т.е. задан угол АСВ в треугольнике АВС и он равен 100/2 = 50 градусов
аналогично рассуждая, получаем второй угол треугольника 120/2 = 60 градусов
очевидно величина третьего угла 180-50-60 = 70 градусов