(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
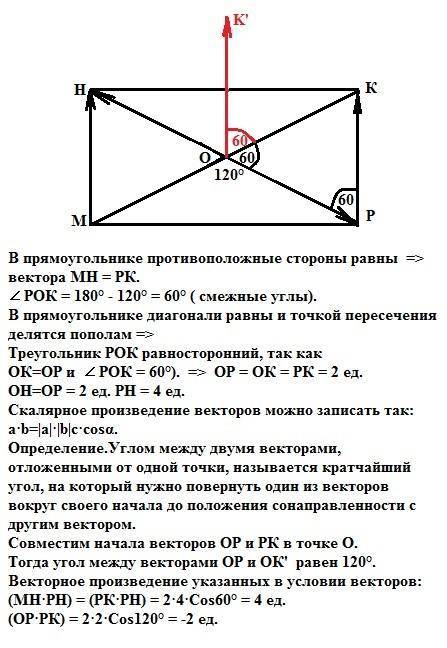
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
Объяснение:
D=2R=12см
α=90°
V- ?
радиус основания конуса
R=D/2=12/2=6 см
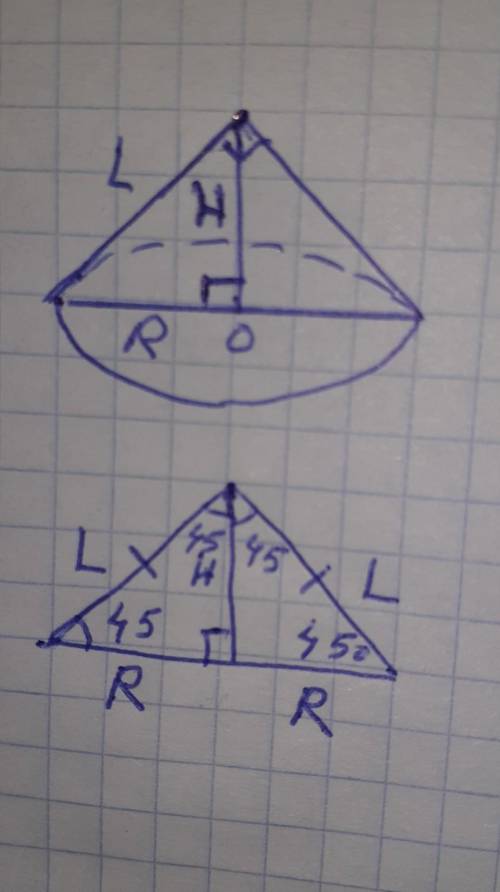
угол при вершине осевого сечения α=90° , то есть прямой угол. значит образующая конуса наклонена под углом 45° к плоскости основания и сечение выглядит как равнобедренный прямоугольный треугольник.
высота конуса равна радиусу основания конуса ,H=R=6см
так как вершина конуса перпендикулярно основанию конуса, и угол при вершине между высотой и образующей конуса 180°-90°-45°=45°
объем конуса
V=1/3 ×πR²×H=1/3 ×π×6²×6=72π см³
или V=72π=72×3,14=226,08 см³
Решение во вложении.