Отрезки AO & OC — радиусы, так как проведены с точек, находящихся на окружности — до центра.
То есть: AO == OC = r.
Стороны друг другу равны, что и означает, что нижние прилежащие углы боковых сторон — тоже друг другу равны(свойство углов равнобедренного треугольника).
<OAC == <OCA = 42° => <AOC (центральный угол) = 180-(42+42) = 96°.
Напротив угла AOC — лежит меньшая дуга AC, а по свойству центрального угла: центральный угол равен градусной мере дуги, противолежащей ей.
То есть: ∪AC = <AOC = 96°.
<ADC — вписаный угол, опирающийся на меньшую дугу AC.
Теорема о вписанном угле в окружности такова: вписанный угол — равен половине градусной меры дуги, на которую он опирается.
То есть: <ADC = ∪AC/2 ⇒ <ADC = 96/2 = 48°.
Вывод: <ADC = 48°.
Відповідь:
3 см
Пояснення:
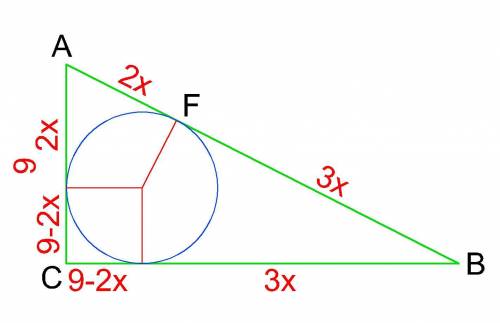
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
S =1/2a×b×sin a
S =1/2×17×8×1/2=34 ,т.к.sin30 гр.=1/2