280 см²
Объяснение:
Найдём диагональ d прямоугольника-основания призмы как гипотенузу в прямоугольном треугольнике, образованном сторонами основания и его диагональю. Она является проекцией диагонали призмы на основание, а также катетом в прямоугольном треугольнике, образованном катетом - ребром призмы (равным высоте призмы) , катетом - диагональю основания и гипотенузой - диагональю призмы.
d=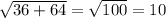
Прямоугольный треугольник, в котором есть внутренний угол 45°, является равнобедренным, поэтому высота призмы равна диагонали основания, как два катета в равнобедренном прямоугольном треугольнике.
Площадь боковой поверхности узнаем, вычислив периметр основания и умножив его на высоту призмы.
Sбок.=P·d=(6+8)·2·10=280 см²
Площадь трапеции равна половине произведения среней линии на выстоту.
Опусим из вершин В и С выстоты BE и CF на основание DA.
BE=CF
Пусть АЕ=х, тогда FD=DA-AE-BC=19-x-5=14-x
По теореме Пифагора находим BE, CF и приравниваем их:
АВ²-х²=CD²-(14-x)²
169-x²=225-(14-x)²
(14-x)²-x²=56
(14-x-x)(14-x+x)=56
14-2x=4
x=5
h=√(169-25)=12см
S=h(BC+AD)/2=12(5+19)/2=144см²
ответ: S=144см²