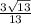Поскольку в условии задачи не указано, лежат ли прямые в одной плоскости или нет, то они необязательно параллельны.
В планиметрии две прямые могут быть параллельными или пересекаться.
Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.
Если две прямые лежат в одной плоскости и не пересекаются, то они - параллельны.
. В стереометрии две прямые могут не пересекаться, но в то же время не быть параллельными.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Скрещивающиеся прямые лежат в параллельных плоскостях, но плоскость провести через них, как это можно сделать через две параллельные прямые, невозможно
Рассмотрим это на ребрах куба (см. приложение)
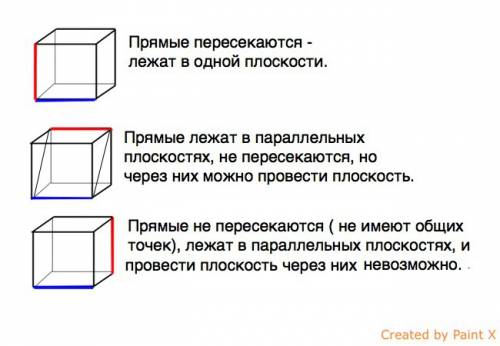
В основании пирамиды лежит квадрат со стороной а, проекция бокового ребра на основания даст половину диагонали квадрата = 12*cos60 = 6 см. Диагональ квадрата
равна 12 см, отсюда сторона квадрата а = 12/√2 см.
Площадь основания a² = 144/2 = 72 см²
Боковая поверхность пирамиды равна площади 4х граней (треугольников) основание которых а, а высота равна апофеме H.
Высота пирамиды находится по боковому ребру h = 12*sin60 = 12*√3/2= 6√3
H=√[(a/2)²+h²] = √[(12/√2)²+(6√3)²] = √(72+12)=√84
s=a*H/2 = 12/√2 * √84/2 = 6√42
Полная поверхность S = 72 + 24√42 ≈ 227,5 см²
ctg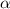 =
= 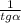 =
= 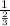 = 1.5
= 1.5
По следствию из основного тригонометрического тождества sin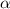 =
= 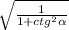 =
= 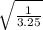 =
= 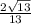
По основному тригонометрическому тождеству cos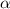 =
= 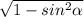 =
=