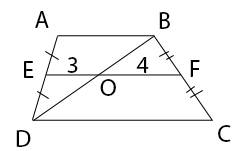
Дано: ABCD - трапеция
EF - средняя линия
EO = 3 см
OF = 4 см
Найти: AB
Решение.
1) Рассмотрим трапецию ABCD. Средняя линия EF параллельна основаниям AB и DC и делит стороны AD и BC трапеции пополам.
2) Рассмотрим треугольники EOD и ABD.
Углы EOD и ABD равны как соответственные при пересечении параллельных прямых EF и AB секущей BD.
Угол DBC общий. Следовательно, треугольник BOF подобен BDC.
3) Из подобия треугольников следует, что
AB / EO = AD / ED => AB = EO * AD / ED = EO * 2ED / ED = EO * 2 = 6 см
По условию задачи в прямоугольном треугольнике АВС гипотенуза АВ = 8 см, ∠С = 90°, ∠ А = 60º, тогда ∠В = 180° - 90° - 60° = 30°
АС – катет, лежащий против угла 30°, равен половине гипотенузы АВ: АС = 1/2 АВ = 8/2 = 4 (см)
Найдем ВС по теореме Пифагора: ВС = √АВ² - АС² = √8² - 4² = √64 - 16 = √48 = 4√3 (см)
ответ: АС = 4 см, ВС = 4√3 см