углы BОD и СОЕ равны
Объяснение:
Мы можем видеть, что у углов АОЕ и ВОF имеется общая часть, угол ВОЕ.
Так как из условия "Углы АОЕ и ВОF на рисунке 45 равны", и мы вычтем из углов их общую чать, то получим, что угол ЕОF равен углу ВОА.
А так как ОВ и OE — биссектрисы углов АОС и DOF, то можем сделать вывод, что угол DOЕ равен углу СОВ.
Углы BОD и СОЕ можно представить как сумму общей для углов части, угол DOС с соответствующими углами СОВ и DOЕ. И так как угол DOЕ равен углу СОВ, следует, что углы BОD и СОЕ равны.
Что и требовалось доказать!
Объяснение:
Так как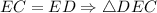 - равнобедренный ⇒
- равнобедренный ⇒ 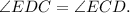
В параллелограмме противоположные стороны параллельны.
При пересечении двух параллельных секущей, накрест лежащие углы равны.
Но так как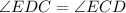 , по свойству ⇒
, по свойству ⇒
Так как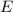 - середина
- середина 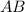 ⇒
⇒ 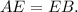
⇒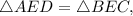 по 1 признаку равенства треугольников.
по 1 признаку равенства треугольников.
⇒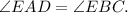
В параллелограмме сумма односторонних углов равна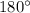 .
.
Т.к.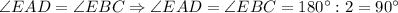 .
.
В параллелограмме сумма односторонних углов равна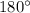 .
.
⇒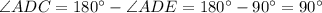
⇒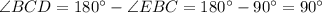
Параллелограмм, у которого все углы прямые - прямоугольник.