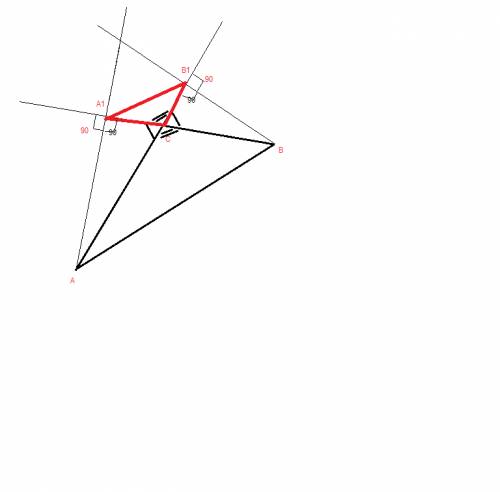
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
Мера двугранного угла равна 60°.
Объяснение:
Определение: Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Пусть дана точка Q на одной из граней двугранного угла. Опустим перпендикуляр QР на ребро АВ этого угла и перпендикуляр QH на вторую грань. Соединим точки Н и Р.
НР перпендикулярна прямой АВ по теореме о трех перпендикулярах. Треугольник QHP - прямоугольный, а мерой двугранного угла является градусная мера угла QPH по определению. Косинус этого угла равен отношению прилежащего катета к гипотенузе, то есть Cos(<QPH) = QH/QP = 1/2 (так как QP = 2*QH по условию).
ответ: <QPH = arccos(1/2) = 60°.