S = 14 ед.²
V = 3 ед.³
Объяснение:
Рассмотрим более простой по форме прямоугольный параллелепипед с длиной а=2, высотой h=2 и шириной b=1.
Площадь такой фигуры состоит из 4 равных боковых граней, размером 2х1 и равных фронтальной и тыльной граней, размером 2х2.
Тогда площадь S₁ всей фигуры равна: S₁ = 4*2*1 + 2*2*2 = 16 ед.²
Объём V₁ такой фигуры равен:
V₁ = a*b*h = 2*1*2 = 4 ед.³
Определим, на сколько меньше площадь S₂ и объём V₂ фигуры, данной в условии, площади S₁ и объёма V₁ прямоугольного параллелепипеда.
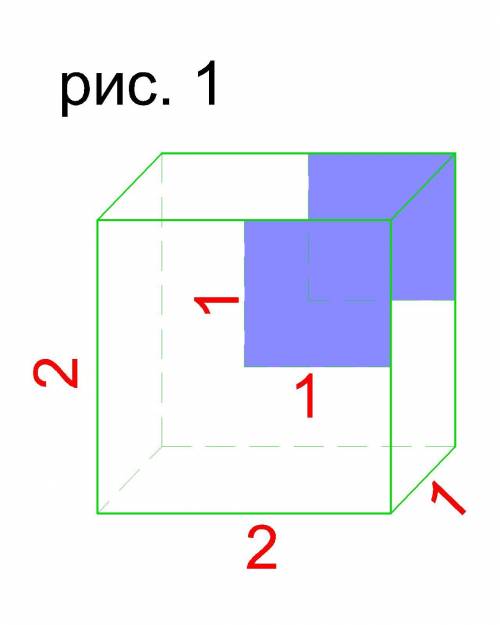
Рассмотрим Рисунок 1.
Из него видно, что S₂ меньше чем S₁ на 2 квадрата размером 1х1 ед.
Тогда S₂ = S₁ - 2*1*1 = 16-2 = 14 ед.²
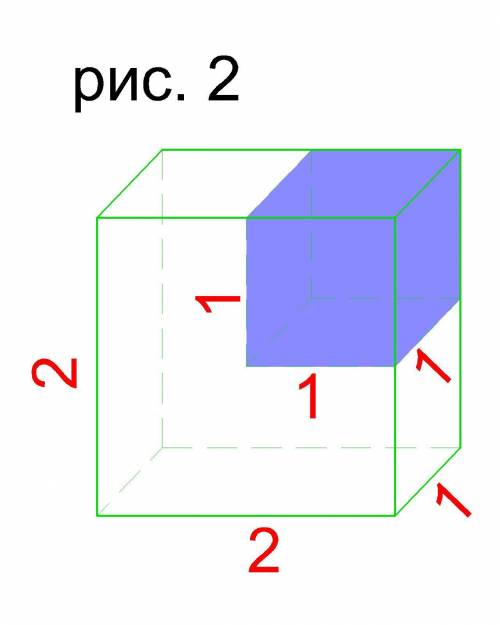
Рассмотрим Рисунок 2.
Из него видно, что V₂ меньше чем V₁ на куб размером 1х1х1 ед.
Тогда V₂ = V₁ - 1*1*1 = 4-1 = 3 ед.³
64 см
Объяснение:
Нам известно что угол В равен 60°. В таком случае угол А будет равен 30°. Катет против 30 равен половине гипотенузы. Что бы найти этот катет мы будем работать в малом прямоугольном ореугольнике СВD. Угол В остаётся равен 60°,значит угол ВСD будет равен 30°. В нем известная нам сторона DB будет катетом против 30. А сторона ВС будет гипотенузой. Находим ее,умножив 16 на 2.
Возвращаемся к большому треугольнику. Теперь нам известно,чему равен катет против 30°. Так как он равен 32 см,при умножении на 2 мы получаем целую сторону АВ,равную 64 см
b) прямая является касательной к окружности.
Объяснение:
Уравнение окружности имеет вид
(x - x₀)² + (y - y₀)² = R², где
(x₀; y₀) - координаты центра окружности,
R - радиус окружности.
(x - 5)² + (y - 10)² = 100
(5; 10) - центр окружности,
R = √100 = 10 - радиус окружности.
а) Окружность изображена на рисунке.
b) Расстояние от центра окружности до прямой у = 20:
d = |y₀ - 20| = |10 - 20| = |- 10| = 10
d = R = 10
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности.