а) В прямоугольной системе координат уравнение сферы радиуса R с центром в точке С(Xo; Yo; Zo) имеет вид:
(x - xo)² + (y - yo)² + (z - zo)² = R².
Значит, надо выделить полные квадраты в заданном уравнении
x² + y² + z² - 4x + 6y = 36.
(x² - 4x + 4) - 4 + (y² + 6y + 9) - 9 + z² = 36.
(x - 2)² +( y + 3)² + z² = 49.
Теперь видны координаты центра сферы: О(2; -3; 0) и величина радиуса R = √49 = 7.
б) Расстояние от центра сферы до заданной плоскости x = −6 равно 2 - (-6) = 8.
Так как радиус равен 7, то сфера не касается такой плоскости.
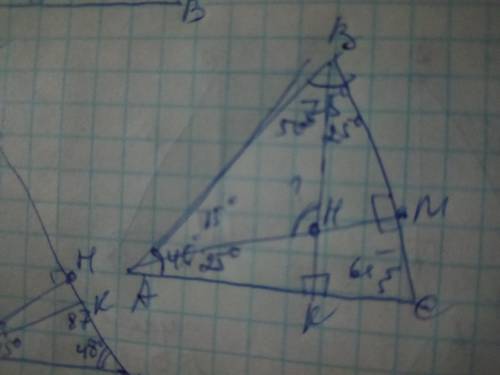
Зная, что ∠ВАС=40°, а угол АВС=75°, и сумма углов треугольника составляет 180°, найдём угол С.
Угол С=180-40-75=65°. Рассмотрим полученный ∆САМ. Он прямоугольный так как УГОЛ АМС=90°, найден угол С=65°, и так как сумма острых углов прямоугольного треугольника составляет 80°, то угол САМ=90-65=25°. Если угол САМ=25°, то угол ВАН=40-25=15°. Рассмотрим ∆СВК. Он также прямоугольный, так как угол ВКС=90°, угол С=65°, поэтому угол СВК=90-65=25°. Если угол СВК=25°, то угол АВН=75-25=50°
Теперь рассмотрим ∆АВН. В нём известны 2 угла: угол ВАН=15°, а угол АВН=50° и можно найти АНВ. Угол АНВ=180-50-15=115°
ОТВЕТ: угол АНВ=115°