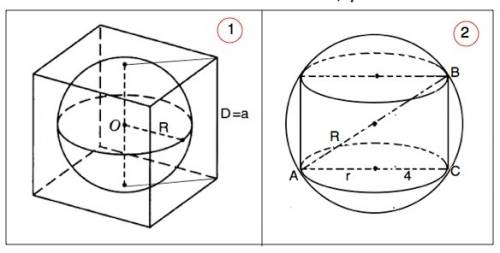
1)
Диаметр вписанного в куб шара равен длине ребра куба, а радиус - половине длины ребра.
Площадь полной поверхности куба равна сумме площадей его 6-ти граней.
Площадь одной грани равна а² =1170/π :6=195/π
R²= (a/2)²=195/4π
Из формулы площади поверхности шара
S=4πR²=4π•195/4π=195 (ед. площади)
2)
Окружности, ограничивающие основания вписанного цилиндра изнутри касаются шара.
Осевое сечение цилиндра - прямоугольник, проходит через центр шара, при этом диаметр шара является диагональю этого прямоугольника.
Из формулы площади поверхности сферы 4πR²=100π находим её радиус R=5 ⇒ D=10
Диаметр основания цилиндра d=2r=8.
Из прямоугольного ∆ АВС высота ( образующая) цилинда ВС=6 ( по т.Пифагора или обратив внимание на отношение катета АС и гипотенузы АВ 4:5 - отношение сторон "египетского" треугольника)
Высота цилиндра - 6 ед. длины.
1) Проводим горизонтальный отрезок произвольной длины.
2) В любой её точке восстанавливаем перпендикуляр длиной, равной заданной высоте. Это первая вершина треугольника.
3) Из конца высоты раствором циркуля, равным длине боковой стороны, делаем засечку на горизонтальной прямой. Получаем вторую вершину треугольника.
4) Из неё раствором циркуля, равным длине боковой стороны, делаем засечку на горизонтальной прямой и получаем третью вершину треугольника.
Можно скомбинировать графический и аналитический методы построения.
Отношение высоты к боковой стороне - это синус угла при вершине.
Найти по синусу угол, разделить его пополам.
Провести перпендикуляр, от его конца отложить полученное значение половины угла при вершине и провести отрезки в обе стороны от перпендикуляра. На них отложить длины боковых сторон и соединить основание.