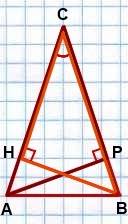
Рассмотрим треугольники ACP и BCH.
1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))
2) ∠C — общий
∠APC=∠BHC=90º (так как AP и BH — высоты (по условию)).
Сумма углов треугольника равна 180º .
В треугольнике ACP
∠CAP=180º — (∠APC+∠C)=180º — 90º — ∠C=90º — ∠C.
В треугольнике BCH
∠CBH=180º — (∠BHC+∠C)=180º — 90º — ∠C=90º — ∠C.
Отсюда,
3) ∠CAP=∠CBH.
Следовательно, треугольники ACP и BCH равны
(по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AP=BH.
Что и требовалось доказать.
В параллелограмме сумма прилежащих к одной стороне углов 180°.
В рабнобокой трапеции углы при основании равны.
В любом параллелограмме противоположные углы равны.
В параллелограмме равны не только углы но и стороны.
В прямоунольной трапеции есть прямые углы.
У квадрата и прямоугольника углы все углы равны.
Диагонали ромба перпендикуларны.
В прямоугольнике диагонали точкой пересечения делят углы пополам.
Диагонали равнобедренной трапеции пересекаются.
Общее свойство для диагоналей прямоугольника и квадрата - равны.