32 ед².
Объяснение:
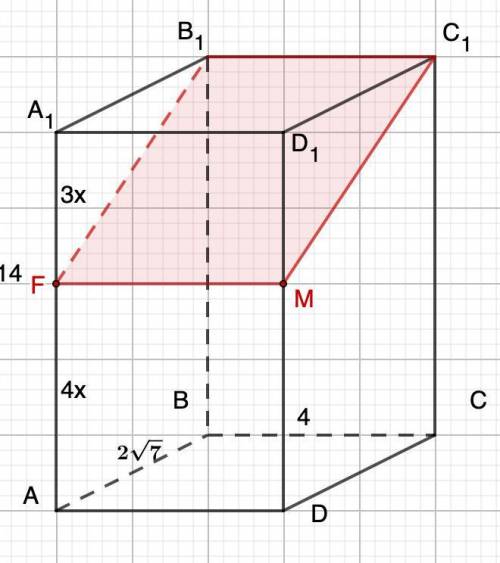
Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.
F∈AA₁, A₁F:FA = 3:4
BC = 4; AB = 2√7; AA₁=14.
Через точки F, B₁,C₁ проходит сечение.
Найти: площадь сечения.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Противоположные грани параллелепипеда параллельны.⇒ сечение FB₁C₁C - прямоугольник.
Площадь прямоугольника равна произведению смежный сторон.⇒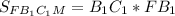 
1. Пусть А₁F = 3x, тогда AF = 4x, а АА₁ = 7х = 14
7х = 14 ⇒ х = 2
Тогда A₁F = 3x = 6
2. Рассмотрим ΔFA₁B₁ - прямоугольный.
A₁F = 6; A₁B₁ = AB = 2√7;
По теореме Пифагора найдем FB₁:
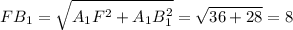
Теперь найдем площадь сечения:
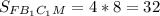(ед.²)
Сторона правильного шестиугольника равна радиусу описанной около него окружности (свойство). Но можно и так: диагонали правильного шестиугольника разбивают описанную окружность на 6 равных равносторонних треугольника (см. рисунок). Поэтому сторона этого шестиугольника равна радиусу описанной окружности.
Rш=10см.
Диагональ правильного четырехугольника (квадрата) равна диаметру описанной около него окружности (свойство). D=20см.
Тогда его сторона равна Rк= 10√2см.
Сторона правильного треугольника равна R*√3 (формула). Или в нашем случае 10√3.
Но можно и без формулы: по теореме косинусов.
a² = 2*R²-2R²*Cos120° или a²=200*(1+1/2) = 100*3. a=√300 = 10√3см.
ответ: сторона треугольника равна 10√3см, четырехугольника10√2см и шестиугольника 10см.