углы BОD и СОЕ равны
Объяснение:
Мы можем видеть, что у углов АОЕ и ВОF имеется общая часть, угол ВОЕ.
Так как из условия "Углы АОЕ и ВОF на рисунке 45 равны", и мы вычтем из углов их общую чать, то получим, что угол ЕОF равен углу ВОА.
А так как ОВ и OE — биссектрисы углов АОС и DOF, то можем сделать вывод, что угол DOЕ равен углу СОВ.
Углы BОD и СОЕ можно представить как сумму общей для углов части, угол DOС с соответствующими углами СОВ и DOЕ. И так как угол DOЕ равен углу СОВ, следует, что углы BОD и СОЕ равны.
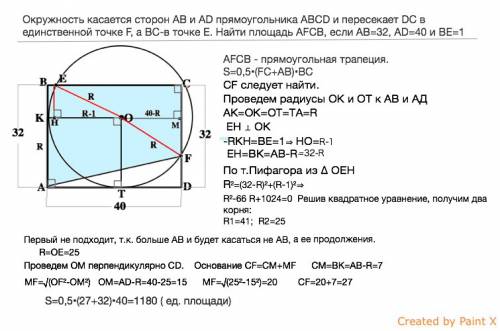
Окружность касается сторон AB и AD прямоугольника ABCD и пересекает DC в единственной точке F, а BC-в точке E.
Найти площадь AFCB, если AB=32, AD=40 и BE=1
————
АBCD- прямоугольник. ⇒
AFCB - прямоугольная трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту.
S=0,5•(FC+AB)•BC
СF следует найти.
Проведем радиусы ОК и ОТ к АВ и АД соответственно.
АК=ОК=ОТ=ТА=R
Опустим из Е перпендикуляр ЕН на радиус ОК
КН=ВЕ=1⇒ НО=R-1
ЕН=ВК=АВ-R=32-R
По т.Пифагора из ∆ ОЕН
R²=(32-R)²+(R-1)²⇒
R²-66 R+1024=0 Решив квадратное уравнение, получим два корня:
R1=41; R2=25
Первый не подходит, т.к. больше, чем АВ, и будет касаться не АВ, а её продолжения.
R=ОЕ=25
Проведем ОМ перпендикулярно СD.
Основание СF=CM+MF
CM=BK=AB-R=7
MF=√(OF²-OM²)
OM=AD-R=40-25=15
MF=√(25²-15²)=20
CF=20+7=27
S=0,5•(27+32)•40=1180 ( ед. площади)
Дано:
a || b
c -секущая
Доказать:
биссектрисы односторонних углов перпендикулярны.
Доказательство.
АЕ - биссектриса угла А,
BD - биссектриса угла В.
АЕ пересекается с BD в точке О.
Известно, что сумма односторонних углов равна 180 градусов, тогда:
Угол А + Угол В = 180
Рассмотрим треугольники АОВ и АОD:
АЕ - биссектриса угла А,
BD - биссектриса угла В.
Угол А и Угол В односторонние =>
Угол ВАО + Угол АВО = 1/2 * (Угол А + Угол В )
Угол ВАО + Угол АВО = 90
Значит Угол АОВ = 180 - (Угол ВАО + Угол АВО) = 180 - 90 = 90
Аналогично и со вторым треугольником.
BD - секущая, a || b => Угол ОВЕ = Углу BDA - накрест лежащие !
Так как углы эти равны, то из равенства Угол ВАО + Угол АВО = 90 следует, что сумма угла А/2 + угол D = 90
Значит угол АОD = 90 =>
трегоьники равны по 3ему признаку равенства треугольников (по трем углам) => АЕ и BD перпендикулярны