1.катеты прямоугольного треугольника равны 5 и 12. определите медиану, проведенную к гипотенузе. 2. катеты прямоугольного треугольника равны 12 и 9. найдите их проекции на гипотенузу. 3.катет прямоугольного треугольника равен 18, а его проекция на гипотенузу 9. найдите длину гипотенузы. 4.проекции
катетов на гипотенузу прямоугольного треугольника равны 2 и 18. найдите высоту треугольника опущенную на гипотенузу. 5.сторона ав равностороннего треугольника авс равна 2√3. найдите ее проекцию на прямую, которой принадлежит высота вн этого треугольника.
Объяснение:
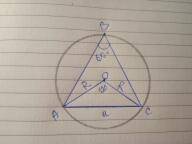
1)Рассмотрим △АВС.
Так как углы при основании АС равны (∠А =∠С), то △АВС - равнобедренный.
В равнобедренном треугольнике боковые стороны равны.
АВ=ВС.
2) Рассмотрим △BDC и △FDE.
BD=DF, CD= ED, ∠EDF =∠CDB - как вертикальные.
Следовательно △BDC = △FDE по двум сторонам и углу между ними ( первый признак равенства треугольников).
Из равенства треугольников следует равенство сторон: BC = EF.
Значит АВ=ВС=EF.
3) Рассмотрим △EHF и △KHF.
EH = KH, ∠EHF =∠KHF, HF - общая.
△EHF = △KHF по двум сторонам и углу между ними ( первый признак равенства треугольников).
Из равенства треугольников следует равенство сторон: EF = FK.
Значит АВ=ВС=EF = FK
Таким образом мы доказали, что АВ = FK
Для доказательства равенства двух отрезков использовали следующие :
Рассматривали эти отрезки как стороны двух треугольников, и доказывали, что эти треугольники равны. Рассматривали эти отрезки как стороны одного треугольника, и доказывали, что этот треугольник равнобедренный.