из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте морфологический разбор нескольких числительных
из упражнения баллов Упражнение 407. Сделайте .
32 cм²
Объяснение:
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок= 1/2*(Р1+Р2)*L,
где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)
Найдём стороны оснований правильной четырехугольной усеченной пирамиды.
Диагональ квадрата: d = a√2, где а - сторона квадрата.
⇒ а = d/√2
АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.
Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.
Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.
Найдем апофему L
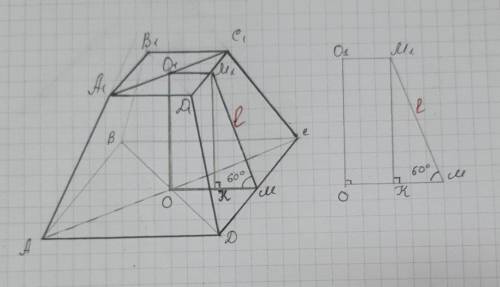
Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.
Т.к. r=a /2 (половина стороны основания), то
О1М1= А1Д1/2 = 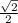
ОМ = АД/2 = 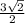
Опустим перпендикуляр М1К из точки М1 верхнего основания на нижнее основание. Получим прямоугольный ΔМ1КМ.
Т.к. М1К⊥КМ, КМ⊥ДС, то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).
КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1= 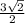 -
- 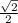 =
=  см.
см.
Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° =  :
: 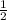 = 2
= 2 cм
cм
Sбок = 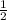 * ( 12
* ( 12 + 4
+ 4 ) * 2
) * 2 =
=  (12+4)
(12+4)  = 2*16=32 cм²
= 2*16=32 cм²
1) угол дае=угол а/2=32 гр.
2)угол дае=углу аде (как углы при осн-и р/б тр-ка аде, а р/б он потому что ае=ед) .
3)угол аед=180-(32+32)=116 (гр) .
ответ: 32 гр, 32 гр, 116 гр.
3