2
Объяснение:
в условии видимо ошибка: в отношении вместо FC нужно FD. Если так, то
Треугольники AFK и EBK подобны, коэффициент подобия 2 ( т.к. AF:BE=2:1). Тогда их высоты относятся как 2:1 и соответственно составляют 1/what и 2/3h, где h - высота параллелограмма к стороне AD.
Обозначим длину стороны AD=BC=a. Тогда AF=2/3a, BE=1/3a.
Значит S треугольника AFK = 1/2(2/3h×2/3a)= 2/9ah
S параллелограмма CEKF= S треугольника BCF - S треугольника BKE = 1/2ah - 1/2(1/3a×1/3h)=1/2ah-1/18ah=8/18ah=4/9ah.
Тогда отношение площадей равно= 4/9ah:2/9ah=2.
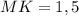 см
см
Объяснение:
Дано: BM - медиана, биссектриса; CN - биссектриса, AB = BC = 5 см,
AC = 6 см
Найти: KM - ?
Решение: Так как по условию BM - медиана, то AM = MC = AC : 2 = 6 : 2 = 3 см. Так как по условию AB = BC, то треугольник ΔABC - равнобедренный. Так как треугольник ΔABC - равнобедренный, то медиана проведенная к основанию является высотой и биссектрисой по теореме. Треугольник ΔCMB является прямоугольным так как
BM ⊥ AC. BM = BK + KM ⇒ BK = BM - MK = 4 - MK.
Так как по условию CN - биссектриса, то по теореме о биссектрисе для треугольника ΔCMB:
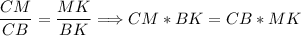
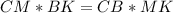
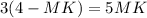
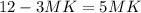
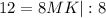
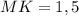 см.
см.
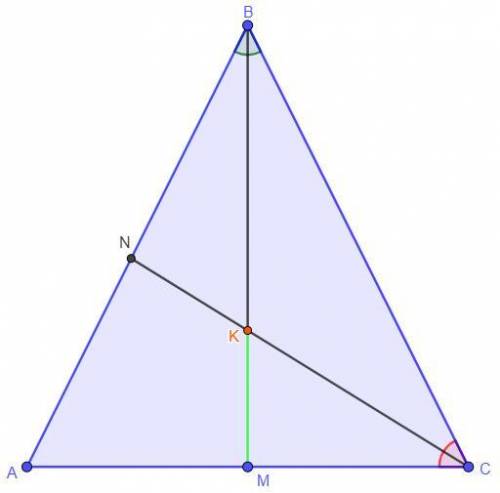
Нет так как у них одна сторона общая значит чтобы их можно было назвать подобными и другие стороны должны быть равными тогда коэффициент подобия равен 1
А другие стороны отличаются