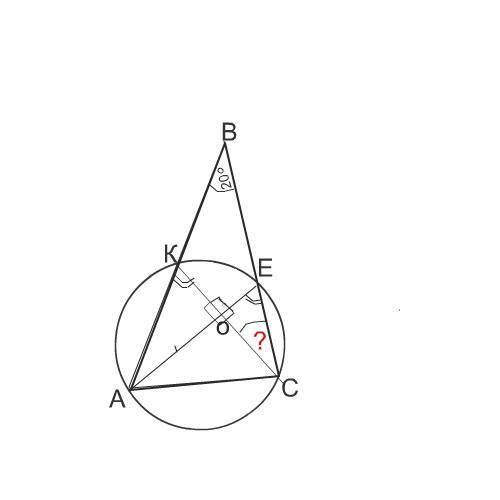
Сделаем рисунок к задаче.
Рассмотрим треугольники АКС и АЕС. Углы при К и Е в них равны, так как являются вписанными углами опирающимися на одну и ту же дугу, стягиваемую хордой АС.
Следовательно углы ВКС и ВЕА тоже равны как смежные с ними.
Угол КОЕ прямой по условию задачи.
Сумма углов четырехугольника равна 360°
Сумма равных углов ВКС и ВЕА равна
360-90-20=250°
Углы эти равны по 250:2=125°
Смежные с ними углы АЕС и АКС равны по 180-125= 55°
Сумма углов треугольника равна 180°
Так как угол ЕОС прямой, угол КСВ равен 180-90-55=35°
КМ ║ТР║ АС⇒ соответственные углы, образованные при их пересечении секущей АВ, равны, а угол В для всех трех треугольников общий.
∆ АВС ~ ∆ТВР~∆ КВМ по двум углам, прилежащим к одной стороне.
АВ=3 части, ТВ=2 части. КР=1 часть.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
АВ:ТВ=3:2=k₁
S ∆ ABC:S ∆ TBP=k₁²=9/4
AB:KB=3:1=k₂
S ∆ ABC:S ∆ KBM=k₂²=9/1
TB:KB=2:1=k₃
S ∆ ТВР: S∆ КВМ=k₃²=4/1