1. Могут.
2. б) 6 см
3. б) 45°
Объяснение:
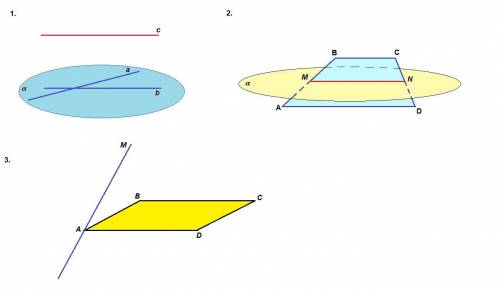
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б) 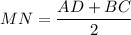
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
а) ВС лежит в плоскости (АВС),
МА пересекает (АВС) в точке А,
А не лежит на прямой ВС, значит
МА и ВС скрещивающиеся.
б) ∠(МА, AD) = 45° по условию,
BC║AD, значит
∠(МА, ВС) = 45°
ответ: 60° и 120°
Свойство диагоналей ромба: они пересекаются под прямым углом, и точкой пересечения делятся пополам.
Рассмотрим образовавшиеся прямоугольные треугольники, катеты 7см и 7√3 см (диагонали пополам)
tg=7/7√3=1/√3 ⇒ ∠1 = 30°
Т.к. сумма острых углов прямоугольного треугольника равна 90°, значит∠2 = 90°-30°=60°
А теперь рассмотрим равнобедренные прямоугольники, образованные двумя прямоугольными. По свойству высоты равнобедренного треугольника, она является и биссектрисой, а значит диагонали ромба являются биссектрисами углов. 30°*2=60°; 60°*2=120°