1) сумма углов АВН и САВ = 180, по теореме, значит АВН = 180-130 = 50
2) точка Т образует с серединами сторон АВ и ВС отрезки, равные 5, это доказывается тем, что угол А 60, а АТ и АР (Р - середина АВ) равны друг другу, а также = 5. Значит треугольник АРТ - равносторонний. Значит сумма длин отрезков (которую требовалось найти) = 10
3) угол ВОС = 90 - 60 = 30, т.к. АОС = 90, угол СОД = 90 - 30 = 60 по такой же причине, значит угол ВОД = 90, угол АОС тоже 90 (по условию), АО=ОС=ВО=ОД, значит треугольники АОС и ВОД равны(по одному из признаков равенства треугольников (две стороны и угол между ними)), значит АС=ВД
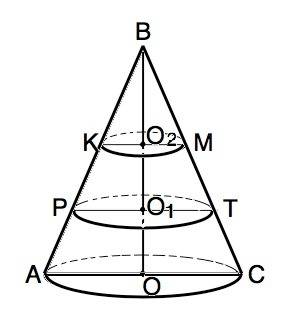
Два сечения, параллельных основанию конуса, делят его на три подобных фигуры. Высота меньшего ВО2=1/3 высоты исходного. Высота среднего ВО1=2/3 высоты исходного. Высота исходного ВО=1=3/3.
Отношение объемов подобных фигур равно кубу коэффициента подобия их линейных размеров. Для верхних двух конусов k=ВО1:ВО2=2 ⇒ V(РВТ):V(КВМ)=k³=8:1.
Объем средней части (усеченного конуса РКМТ)=V (РВТ)-V (КВМ), что соответствует 8V (квм)-1V (квм)=7V (квм). ⇒ V (КВМ)=14:7=2. Объем меньшего конуса 2 (ед. объема).
Отношение высоты исходного конуса к высоте меньшего k=3:1, следовательно, k³=27.
Объем искодного конуса 27•2=54 (ед. объема)
Меньшая дуга АВ лежит против центрального угла 20°, значит большая дуга лежит против угла 360°-20°=340°. Этот угол больше ∠АОВ в 340/20=17 раз, значит и большая дуга в 17 раз больше, то есть 88х17=1496