они действительно равны
Объяснение:
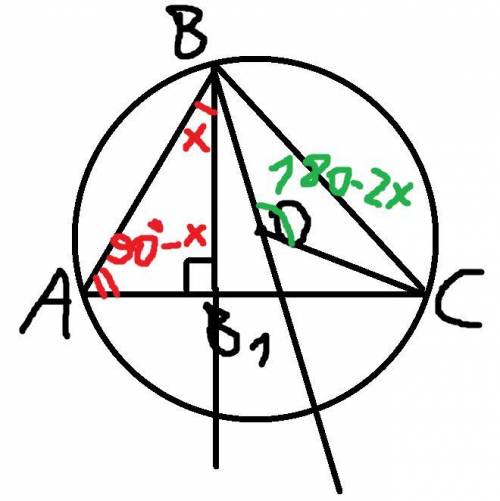
Пусть <ABB1 = x, тогда если <BB1A = 90 градусов (т.к. BB1 - высота), то ABB1 = (180 - 90 - x) градусов = (90 - x) градусов. Т.к. <BAC - вписанный для дуги BC, а <BOC - центральный для этой же дуги BC, то <BOC = 2*<BAC = 2*(90 - x)градусов = (180 - 2x) градусов. Очевидно, что BO = OC = R, тогда треугольник BOC - равнобедренный, тогда <CBO = <BCO = (180 - < BOC) / 2 = (180 - (180 - 2x)) / 2 = 2x / 2 = x. Следовательно <ABB1 = <CBO = x.
1.
Треугольники: ВОС, DОА, АОВ
Т. К. ABCD квадрат, диагонали делят квадрат на 4 равные треугольника
2. ВАD = 80°
Т.к. ABCD ромб, Диагонали ромба являются биссиктрисами =>
АВD = 2×CAD
ABD = 40×2 = 80
4. P = 32 cм
ABCD ромб, Диагонали в точке пересечения делятся пополам, АС перпендикулярна ВD => ВD = OD
AOD прямой треугольник
Угол А = 30° => АО = 2ОD
AO = 2×4 = 8 см
P = 8×4 = 32 см
5 ABCD прямоугольник => АВ = СD; BC = AD
Биссиктрисами в прямоугольнике отделяет равнобедренный треугольник
Треугольник АВК р/б => АВ=ВК = 8
ВС = ВК + КС
ВС = 8+3 =11 см
Р = 2× (11 + 8) = 19×2 = 38 см
Прости я слепая, не увидела, что только 2 и 5...