(см. объяснение)
Объяснение:
Первая система уравнений:
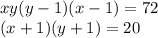
Раскроем скобки:
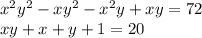
В первой строке вынесем xy за скобки, а из второй выразим x+y:
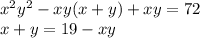
Теперь подставим x+y из второго уравнения в первое:
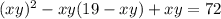
Делаем замену вида 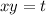 :
:
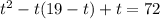
Решим это уравнение:
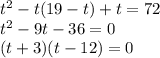
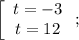
Получили две сильно упрощенные системы:
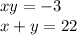 или
или 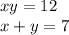
Для первого случая:

Для второго случая:
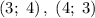
Итого исходная система имеет четыре решения:
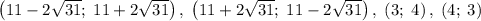
Система уравнений решена!
Вторая система уравнений:
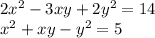
Умножим первое уравнение на 5, а второе на 14:
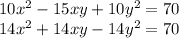
Теперь приравняем левые части:
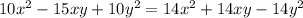
Выполним преобразования:
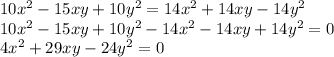
Теперь есть два подхода к решению:
Делим все уравнение на y², вводим замену вида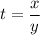 и решаем уравнение
и решаем уравнение 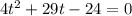 . После чего получаем, что
. После чего получаем, что 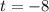 или
или  . Дальнейшие действия очевидны.Разложим уравнение на множители, заметив, что
. Дальнейшие действия очевидны.Разложим уравнение на множители, заметив, что 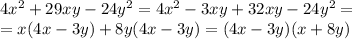 .
.Я рекомендую пользоваться первым .
Итак, имеем две системы:
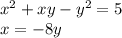 или
или 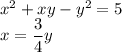
Для первого случая:
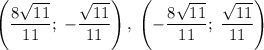
Для второго случая:
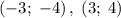
Итого исходная система имеет четыре решения:
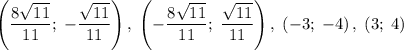
Система уравнений решена!
Задание выполнено!
Пусть дан четырёхугольник АВСD. Точка К - середина АВ, т.М - середина ВС, N и Т - середины СD и DA соответсвенно. По условию КN=ТМ. Проведем диагонали АС и ВD. Соединим середины сторон треугольников АВС, ВСD, CDA и DAB. В треугольниках АВС и АDC средние линии параллельны и равны половине диагонали АС исходного четырехугольника.⇒ КМ параллельна и равна ТN. Аналогично доказывается КТ=МN. Противоположные стороны КМNТ параллельны и равны. КМNТ - параллелограмм с равными диагоналями ( КN=МТ по условию), т.е. КМNТ - прямоугольник. А раз стороны КМNТ пересекаются под прямым углом, то и диагонали четырехугольника АВСD, которым они параллельны, также пересекаются под прямым углом, ч.т.д.